Benutzer-Werkzeuge
Seitenleiste
Dies ist eine alte Version des Dokuments!
Inhaltsverzeichnis
Dokumentation des "Produkts"/ Projektergebnisses
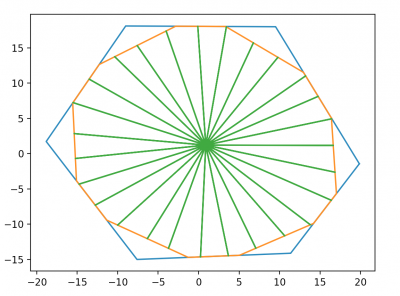
1. Die Netzstruktur des Radnetzes
Das fertige Radnetz besteht aus vier Komponenten:
- einem äußeren Netzring, dessen Eckpunkte die Ankerpunkte an der Umgebung darstellen sollen
- einem inneren Netzring, der die Belastung die beim Fangen von Beute entsteht gleichmäßiger verteilt, um die Ankerpunkte nicht zu überlasten.
- den Speichen, die strahlenförmig vom Mittelpunkt des Netzes zum inneren Ring verlaufen
- der Fangspirale, die sich engmaschig um die Speichen windet und als einziger Teil des Radnetzes dazu dient, tatsächlich die Beute zu fangen
äußerer Netzring
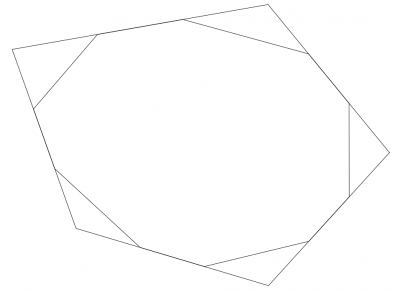
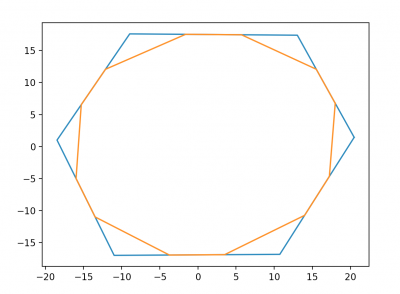
Der äußerer Netzring ist meist ein einfaches Polygon, das den Kontakt des Netzes zur Außenwelt herstellt, und eine rein strukturelle Funktion hat. Die Anzahl der Ecken ist von der Spinnenarm und der Umgebung abhängig.

innerer Netzring
Mit dem inneren Netzring ist diejenige From gemeint, die entsteht, nachdem alle Ecken des äußeren Netzringes durch Querverbindungen vom Netzinneren getrennt wurden. Das entlastet die einzelnen Ecken, indem es die Kraft eines gefangenen Insekts besser auf alle Ecken verteilt.
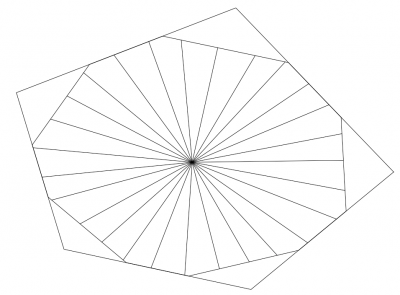
Speichen
Die Speichen sind sternförmig vom Netzmittelpunkt ausgehende Fäden, die am inneren Netzring ansetzen und die Basis für das Eigentliche Fangnetz bilden.
Fangspirale
Die Spirale ist der einzige Teil des Netzes, der Tatsächlich klebt und damit Beute fangen kann. die Spirale eines Netzes ist selten perfekt; die Spinnen verändern ihre Form, um optimal die Fläche des Netzes auszunutzen oder Schäden zu reparieren. Für unser Projekt haben wir die dabei entstehenden Spiralformen vereinfacht, um sie für uns umsetzbar zu machen:
eine tatsachlich runde Spirale
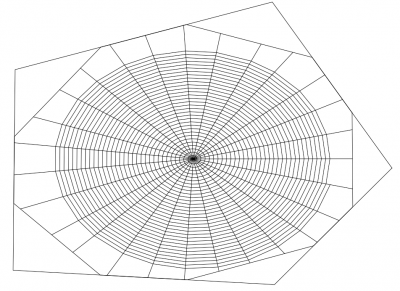
und eine die möglichst viel Fläche abdeckt
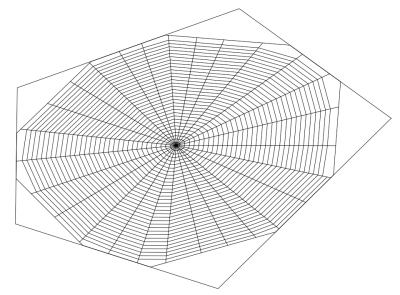
2. Umsetzung im Programm
äußerer Netzring
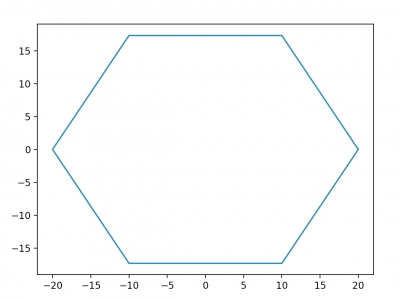
Der Äußere Netzring wird relativ einfach in zwei Schritten generiert:
Zuerst werden n Punkte (wieviele Eckpunkte das Netz hat ist variabel) gleichmäßig auf einem Kreis verteilt, wobei Mittelpunkt und Radius im Konstruktor der Klasse angegeben werden:
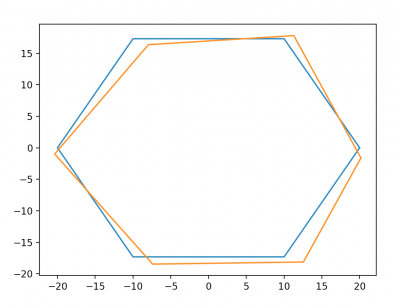
Danach werden die Punkte um einen zufälligen Wert in eine zufällige Richtung verschoben, wobei die Zufallswerte so angelegt sind, das das Netz nicht all zu deformiert werden kann:
Zuletzt wird der Mittelpunkt neu berechnet, als Mittelwert aller Eckpunkte.
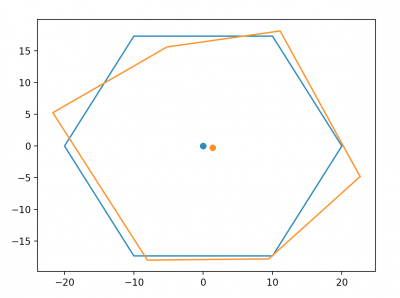
innerer Netzring
Die Querverbindungen des inneren Netzrings beginnen auf genau 1/3 und 2/3 des jeweiligen Abschnitts des äußeren Netzrings. Sie werden durch gewichtete Mittelwerte aus den Eckpunkten des äußeren Netzrings errechnet ( (2A + B)/3 und (A + 2B)/3 ).
Speichen
Die Speichen sollen vom neuen Mittelpunkt ausgehend bis zum inneren Netzring verlaufen, unabhängig von dessen Eckpunkten, und ihre Anzahl soll frei Variable sein. Dazu wird eine Liste von Winkeln erzeugt, die die Speichen später haben sollen. In diesen Winkeln vom Mittelpunkt ausgehend wird der Schnittpunkt mit dem inneren Netzring gesucht.