Benutzer-Werkzeuge
Seitenleiste
Inhaltsverzeichnis
Optimierungsprogramm
Ziel
Ein Programm, welches eine 3d Erhöhungsdatei, sowie zwei Punkte als Input nimmt und den kürzesten Weg zwischen den Beiden Punkten ausgibt.
Ergebnis
Teilnehmer
Vollständige Dokumentation: Berechnung des kürzesten Weges zwischen zwei Punkten
Im Rahmen des MINTGrün Projektlabors Mathesis an der TU-Berlin im Wintersemester 14/15 haben wir uns mit einer klassischen Optimierungsaufgabe befasst: den kürzesten Weg über eine realistische 3D-Oberfläche zu finden. Die Funktionsweise dieses Python-Programms wird im folgenden erklärt.
Betrachten wir die Datei run.py und gehen chronologisch durch die Struktur bis zur Lösung.
Es beginnt die Main-Methode. Notwendige Übergabeparameter sind eine Liste aus Zahlenwerten, die die Z-Werte der Koordinaten von der 3D-Oberfläche darstellt, Start-und Zielpunkt der Berechnung, und eine Auflösung mit der Kanten diskretisiert werden.
from __future__ import division def main(asciidatei,startpoint,endpoint,aufloesung): from datenstruktur import datenstruktur punktliste,delaunay,dreiecksliste,kantenliste=datenstruktur(asciidatei,aufloesung)
Die Datenstruktur
Die Datei datenstruktur.py erstellt zunächst aus allen Z-Werten des Input-Arrays Punkte mit XYZ-Werten, anschließend werden diese Delaunay-trianguliert und aus den entstehenden Dreiecken werden noch die Kanten erstellt. Diese Kanten werden zusätzlich noch diskretisiert (in kleine Teile aufgeteilt) und es werden Unterpunkt-Objekte auf der (mit der Anzahl 'aufloesung' in Main-Methode) Kante erstellt. Dabei enstehene folgende Objekte mit folgenden Attributen:
Punkt
- self.xy:Ursprungsvektor in 2D
- self.xyz:Urpsrungsvektor in 3D
- self.borderingTriangles:Liste der Dreiecke, deren Teil dieser Punkt ist
Dreieck
- self.p1,self.p2,self.p3:Die 3 Punkte die das Dreieck beschreiben als Punkt-Objekte
- self.borderingKanten:Liste der Kanten, aus denen dieses Dreieck besteht als Kanten-Objekte
- self.normal:Normalvektor der Ebenengleichung des Dreiecks, notwendig um die Z-Koordinate eines inneren 2D Punktes zu ergänzen
Kante
- self.p1, self.p2: Die 2 Punkte, die die Kante beschreiben als Punkt-Objekte
- self.borderingTriangles:Liste der Dreiecke, deren Teil diese Kante ist, als Dreiecks-Objekte
- self.vektorxy: Richtungsvektor der Kante in 2D
- self.vektorxyz: Richtungsvektor der Kante in 3D
- self.borderingKanten: Liste der Kanten in den beiden Dreiecken, deren Teil diese Kante selber ist. In dieser Liste darf die Kante selber nicht enthalten sein
- self.unterpunkte: Liste der Unterpunkte auf der Kante als Unterpunkt-Objekte
- self.maximum: Der Betrag der Distanz des besten (bis jetzt gefundenen) Weges vom Anfangspunkt der Berechnung zu dem Unterpunkt dieser Kante, der am Weitesten vom Anfangspunkt entfernt liegt. Der Konstruktor setzt diesen wert auf 0, er wird bei der Berechnung durch andere Werte ersetzt
- self.minimum: Der Betrag der Distanz des besten (bis jetzt gefundenen) Weges vom Anfangspunkt der Berechnung zu einem Unterpunkt auf dieser Kante. Der Konstruktor setzt diesen Wert zunächst auf Unendlich
- self.history: Zunächst auf [0] gesetzt, mehr dazu im Bereich Lösungsalgorithmus
- self.fertig: Zunächst auf False gesetzt, mehr dazu im Bereich Lösungsalgorithmus
- self.front: Zunächst auf False gesetzt, mehr dazu im Bereich Lösungsalgorithmus
- self.zubetrachtend: Zunächst auf False gesetzt, mehr dazu im Bereich Lösungsalgorithmus
Unterpunkt
- self.xyz: Ortsvektor dieses Unterpunktes in 3D
- self.weg: Zunächst leer. Liste aller Unterpunkte, über die der bis jetzt gefundene Optimale Weg vom Anfangspunkt bis zu diesem Unterpunkt führt
- self.distanz: Betrag der Distanz zwischen allen Punkten in self.weg
Der Lösungsalgorithmus
Prinzipiell beruht die Lösung unseres Problemes auf einer modifizierten Version des Dijkstra-Algorithmus. Wir gehen von einem Anfangspunkt aus, und ermitteln in welchem Dreieck er liegt (indem wir das Minimum der Distanzen von diesem Anfangspunkt zu den drei Eckpunkten jedes Dreiecks in der Dreiecksliste finden). Wir wissen auch, aus welchen Kanten dieses Dreieck besteht.
Weiterhin wichtig ist die Datei berechnung.py berechnung.py nimmt zwei Kanten als Input und berechnet den kürzesten Weg von jedem Punkt auf der ersten Kante zu jedem Punkt auf der zweiten Kante. Diese Berechnung ist rechenaufwendig und wurde deshalb mit cython in C übersetzt. Dabei gibt es die Möglichkeit, dass bessere Wege zu jedem Unteprunkt auf dieser Kante gefunden werden, als es bisher gab (wenn es vorher noch keinen berechneten Weg gab, wird er auf jeden Fall ersetzt). Wenn kein einziger Punkt bei einer Berechnung zwischen zwei Kanten ersetzt wurde (sprich, jeder bereits vorhandene Weg zu dieser Kante war besser als der in dieser Berechnung gefundene), wird die zweite Kante returned, ansonsten wird 0 returned.
#Init of Cython, notwendig um anfang.py bzw. berechnung.py auszuführen import pyximport pyximport.install() #Anfangskanten finden from anfang import anfang anfangskanten,anfangsdreieck=anfang(startpoint,dreiecksliste) #Endkanten finden from endpunkt import endpunkt endkanten,enddreieck=endpunkt(endpoint,dreiecksliste)
Es werden also die drei Kanten des Anfangsdreiecks gefunden und es wird eine Berechnung zu ihnen durchgeführt.
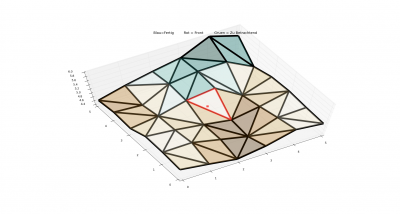
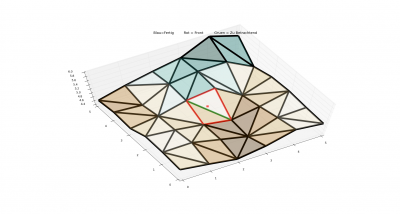
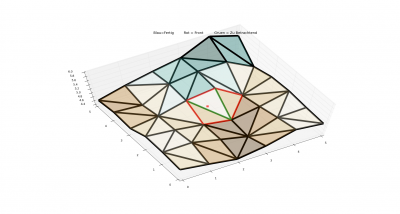
Näherungsweise kann man sich den Algorithmus wie eine Art Welle vorstellen, die sich immer dort weiter ausbreitet, von wo die Distanz zum Anfangspunkt am kleinsten ist. Kanten können prinzipiell 4 Zustände haben:
- Keinen - da sie momentan für die Berechnung noch nicht relevant sind
- Front - Eine Kante dessen Front-Attribut True ist, kann man sich wie die Wellenfront vorstellen. Dies sind die äußersten Kanten die momentan relevant sind. Es wird immer von der Kante in der Front weitergerechnet, für die gilt, dass ihr Kante.minimum kleiner ist als das minimum Attribut von allen anderen Kanten in der Front.
- Zubetrachtend - Kanten dessen Zubetrachtend-Attribut True ist, waren schon mindestens einmal in der Front und es wurde schon einmal eine Berechnung zu dieser Kante durchgeführt. Es ist aber nicht ausgeschlossen, dass noch bessere(hier:kürzere) Wege vom Anfangspunkt zu Punkten auf dieser Kante gefunden werden können.
- Fertig - Für Kanten, dessen Fertig-Attribute True ist, gilt, dass der Optimale Weg vom Anfangspunkt zu jedem Punkt auf dieser Kante schon gefunden wurde. Das gilt per Definition, wenn der längste bestehnde Weg vom Anfangspunkt zu irgendeinem Punkt auf dieser Kante kürzer ist, als der kürzeste Weg zu irgendeiner Kante in der Front.
Wir können eindeutig sagen, dass wir den Optimalen Weg von Anfangspunkt zum Endpunkt gefunden haben, wenn alle drei Endkanten Fertig sind. Die Schleife unseres Algorhitmus, welche einen Schritt weiterrechnet, wird also dann unterbrochen wenn diese Bedingung erfüllt ist. Zu Beginn sind Front und Zubetrachtend gleich den drei Anfangskanten, und noch keine Kante ist fertig.
#Erstellen der Input-Listen from copy import copy zubetrachtend=copy(anfangskanten) front=copy(anfangskanten) fertig=[] from schleife import schleife while (endkanten[0].fertig==False or endkanten[1].fertig==False or endkanten[2].fertig==False): zubetrachtend, front, fertig=schleife(zubetrachtend,front,fertig)
Die Schleife
Diese Schleife, enthalten in schleife.py verläuft wie folgt:
Zunächst wird das erste Element der Liste aller Kanten in der Front gewählt. Diese Liste ist sortiert, so dass das erste Element die Kante mit dem kleinsten Minimum, also dem kürzesten Weg zum Anfangspunkt ist. Es wird für alle an dieser Kante angrenzenden Kanten in pruefung.py geprüft:
- Dass sie noch nicht Fertig sind
- Dass dies nicht die Kante ist, von der die Berechnung im letzten Schritt hergekommen ist
- Dass diese Kante nicht im Schritt davor von der selben Kante hergekommen ist, wie die Kante die wir gerade betrachtend (das erste Element der Front)
def pruefung(kante1,kante2): if (kante2.fertig==True): return False if len(kante2.history!)=0: if (kante2.history is kante1) or (kante2.history is kante1.history): return False return True
Wenn also pruefung.py ein True wiedergibt, dann ist es sinnvoll, eine Berechnung zu dieser Kante durchzuführen. Wenn bei dieser Berechnung mindestens ein besserer Weg zu einem Unterpunkt gefunden wurde (sprich: berechnung returned 0), wird diese Kante also in die Front aufgenommen. Dazu wird sie zunächst entfernt, wenn sie schon in der Front enthalten ist, und dann mit der Funktion reinpacken.py wieder an der richtigen Stelle, nach dem Wert des Minimums, in die Liste einsortiert. Nachdem dies für alle Kanten, die an dem ersten Element von Front angrenzen geschehen ist, wird diese Kante aus der Front genommen und in zubetrachtend richtig einsortiert.
def schleife(zubetrachtend,front,fertig): from pruefung import pruefung from berechnung import berechnung from reinpacken import reinpacken from copy import copy #Sucht Kanten für die es Sinn macht, eine Berechnung durchzuführen. bk=copy(front[0].borderingKanten) for borderingkante in bk:#front[0].borderingKanten: if (pruefung(front[0],borderingkante)==True): nichtweiterrechnen=berechnung(front[0],borderingkante) #Wenn mindestens ein Punkt ersetzt wurde: if nichtweiterrechnen==0: if borderingkante in front: front.pop(front.index(borderingkante)) front=reinpacken(front,borderingkante) borderingkante.front=True #Nimmt diese Kante aus der Front und weist sie zubetrachtend zu front[0].front=False front[0].zubetrachtend=True zubetrachtend=reinpacken(zubetrachtend,front.pop(0))
Danach müssen alle Kanten darauf geprüft werden, ob sie in diesem Schritt fertig geworden sind. Kanten, die am Rand der Karte sind (die nur an einem Dreieck angrenzen, werden zunächst aus der Front herausgenommen und zubetrachtend hinzugefügt. Danach werden alle Zubetrachtenden Kanten darauf geprüft, ob sie Fertig sind. Zunächst wird geprüft ob diese Kanten am Rand der Karte liegen, woraufhin sie als Fertig definiert werden. Danach wird geprfüt ob es überhaupt noch ein Element in der Front gibt. Wenn es keins mehr gibt, können keine besseren Wege mehr gefunden werden und alle Kanten werden als fertig definiert. Zudem kann dann die dritte Bedingung nicht erfüllt werden. Wenn es aber noch mindestens ein Element in der Front gibt, sind Kanten genau dann fertig, wenn das Maximum von ihnen kleiner ist als das Minimum des ersten Elements der Front ist.
#Nimmt Kanten aus der Front, die am Rand der Karte sind (nur ein angrenzendes Dreieck) #heraus und fuegt sie Zubetrachtend hinzu index=0 for i in range(len(front)): if (len(front[i-index].borderingTriangles)==1): front[i-index].zubetrachtend=True front[i-index].front=False zubetrachtend=reinpacken(zubetrachtend,front.pop(i-index)) index+=1 #Prüft ob Kanten in zubetrachtend Fertig sind index=0 for i in range(len(zubetrachtend)): if (len(zubetrachtend[i-index].borderingTriangles)==1): zubetrachtend[i-index].fertig=True zubetrachtend[i-index].zubetrachtend=False fertig=reinpacken(fertig,zubetrachtend.pop(i-index)) index+=1 #Wenn Alle Kanten Fertig oder Zubetrachtend sind, dann kann keine Bessere Lösung mehr gefunden werden #Und die dritte Bedingung kann nicht mehr erfüllt werden elif len(front)==0: zubetrachtend[i-index].fertig=True zubetrachtend[i-index].zubetrachtend=False fertig=reinpacken(fertig,zubetrachtend.pop(i-index)) index+=1 #Sonst: maximum der zubetrachtenden Kante kleiner als minimum des kleinsten Elements von front elif (zubetrachtend[i-index].maximum<front[0].minimum+0.0000001): zubetrachtend[i-index].fertig=True zubetrachtend[i-index].zubetrachtend=False fertig=reinpacken(fertig,zubetrachtend.pop(i-index)) index+=1 return zubetrachtend,front,fertig
Die Lösung
Wenn diese Schleife nicht mehr läuft, wird dann noch mithilfe der Funktion ende.py der Unterpunkt auf den drei Kanten des Enddreiecks gefunden, für den gilt, dass die Summe des Weges vom Anfangspunkt zu diesem Unterpunkt und des Weges von diesem Unterpunkt zum Zielpunkt kleinstmöglich ist. Das Attribut weg dieses Punktes hat alle Unterpunkte eingespeichert, die berührt werden, wenn man auf dem optimalen Weg vom Anfangspunkt zum Endpunkt rechnet. Dieser Weg ist also die Lösung.
from ende import ende weg=ende(endkanten,endpoint,enddreieck)
Insgesamt: ohne grafische Darstellung
Insgesamt sieht die datei run.py ohne jegliche grafische Darstellung also aus wie folgt:
from __future__ import division def main(asciidatei,startpoint,endpoint,aufloesung): from datenstruktur import datenstruktur punktliste,delaunay,dreiecksliste,kantenliste=datenstruktur(asciidatei,aufloesung) #Init of Cython, notwendig um anfang.py bzw. berechnung.py auszuführen import pyximport pyximport.install() #Anfangskanten finden from anfang import anfang anfangskanten,anfangsdreieck=anfang(startpoint,dreiecksliste) #Endkanten finden from endpunkt import endpunkt endkanten,enddreieck=endpunkt(endpoint,dreiecksliste) #Erstellen der Input-Listen from copy import copy zubetrachtend=copy(anfangskanten) front=copy(anfangskanten) fertig=[] from schleife import schleife while (endkanten[0].fertig==False or endkanten[1].fertig==False or endkanten[2].fertig==False): zubetrachtend, front, fertig=schleife(zubetrachtend,front,fertig) from ende import ende weg=ende(endkanten,endpoint,enddreieck) return 0
Die Visualisierung
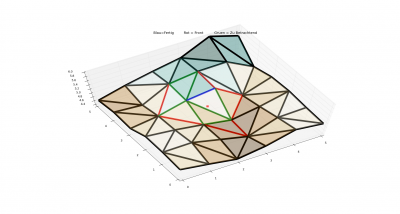
Die Visualisierung wurde mit Python-Matplotlib gemacht. Matplotlib ist zwar auf die dauer ziemlich langsam (am Ende mehr als die Hälfte der runtime), aber ist für simple Darstellungen durch eine übersichtliche API ziemlich nützlich. Rote Kanten sind als Kanten in der Front markiert, Grüne Kanten sind zu betrachtende Kanten, und blaue Kanten sind fertige Kanten (für die der Optimale Weg schon gefunden wurde)
Projektseiten
Literatur
Interessantes Paper zu Geodäten auf polyedrischen Flächen: http://www.polthier.info/articles/straightest/straightest_preprint.pdf
Und eins zur Wellenausbreitung: http://www.polthier.info/articles/geodflow/geodflow_wien99.pdf