Benutzer-Werkzeuge
Seitenleiste
Inhaltsverzeichnis
Koppelnavigation mit Odometriedaten von Robotern mit Differentialantrieb
Viele Roboter im Labor benutzen zur Steuerung und Vorwärtsbewegung zwei unabhängig angetriebene Räder. Hier soll kurz dargestellt werden, wie in einem solchen System die Bewegung des Roboters anhand der Radumdrehungen nachvollzogen werden kann.
Grundlage: Beschreibung der Lage des Roboters im Raum
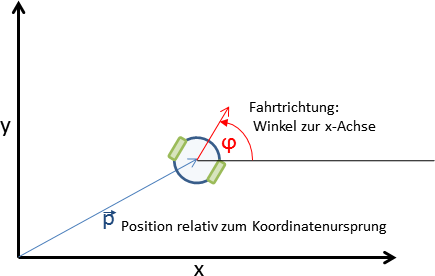
Die Lage des Roboters im Raum (in der Fachliteratur „Pose“ genannt„) wird in unserem einfachen Fall vollständig durch den Abstand des Robotermittelpunkts zum Koordinatenursprung (nennen wir $\vec{p}$) und den gegen den Uhrzeigersinn gemessenen Winkel zwischen Fahrtrichtung und x-Achse ($\varphi_{Roboter}$) beschrieben.
Teil 1: Radumdrehungen in Vorwärts- und Drehbewegung umrechnen
Aus der Ansteuerung der Steppermotoren bzw. durch das Auslesen von Getriebemotorencodern wissen wir, wie weit sich die beiden Räder vor- bzw. rückwärts gedreht haben. Um zu berechnen, wie sich Position und Ausrichtung des Roboters dadurch verändern, zerlegen wir diese Radumdrehungenszahlen in eine Dreh- und eine Vorwärtsbewegung des Roboters.
Dazu betrachten wir zunächst die Grenzfälle von Drehung auf einem Punkt und Geradeausfahrt entlang einer Line.
Zurückgelegte Strecke eines Rades
Grundlage der folgenden Diskussion ist das Bild der Spur vor, die jedes der Räder auf dem Boden abfährt.
Wenn sich das Rad um genau eine Umdrehung dreht, verlängert sich diese Spur $s_{Rad}$ genau um den Umfang des Rades $2\pi r_{Rad}$. Für einen kleineren oder größeren Drehwinkel $\varphi_{Rad}$ wird genau der Anteil des Umfangs zurückgelegt, der dem Anteil des Winkels am Gesamtkreis entspricht.
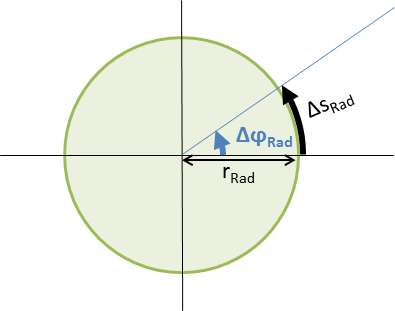
\[\Delta s_{Rad}=\Delta\varphi_{Rad}*r_{Rad}\]
Reine Vorwärtsbewegung
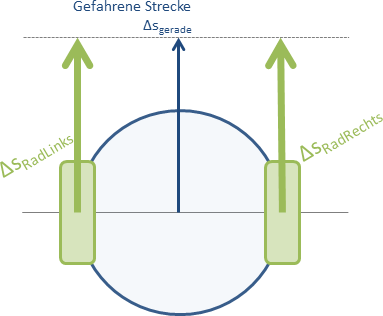
Wenn beide Räder eine gleiche Strecke in die gleiche Richtung zurückgelegt haben, ist die Sache simpel:
Der Schwerpunkt des Roboters bewegt sich in diesem Fall genau die Abgewickelte Strecke der Radumdrehung in seine Blickrichtung:
\[\Delta s _{gerade}=\Delta s _{Rad} \]
Drehung auf der Stelle
Als nächstes stellen wir uns vor, dass sich die beide Räder gleich weit in entgegengesetzte Richtungen drehen.
Der Roboter dreht sich dabei auf der Stelle, wobei sich seine Räder auf einem Kreis bewegen, dessen Durchmesser dem Abstand der beiden Räder entspricht.
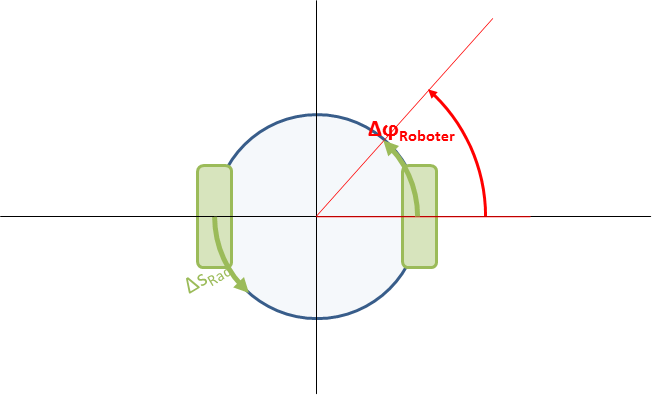
Die Länge der Spur $s_{Rad}$, die jedes der Räder während einer vollen Umdrehung des Roboters (entspricht $\Delta \varphi_{Roboter}=2\pi$ um sich selbst auf dem Boden abfährt, ist daher genau gleich dem Umfang eines Kreises mit Roboterdurchmesser ($2\pi * r_{Roboter}$).
Es gilt also: \[ \Delta \varphi_{Roboter}=2\pi \Leftrightarrow \Delta s_{Rad}=2\pi * r_{Roboter}\Leftrightarrow 2\pi=\frac{\Delta s_{Rad}}{r_{Roboter}}\]
Bzw. für Anteile einer vollen Drehung: \[\Delta \varphi_{Roboter} = \frac{\Delta s_{Rad}}{r_{Roboter}}\]
Mischung aus Vorwärtsbewegung und Drehung
Was tun, wenn sich die beiden Räder eben nicht genau gleich weit gedreht haben?
Ganz einfach: Wir zerlegen die zurückgelegten Strecken der beiden Räder in einen Anteil $\Delta s_{gerade}$, der für beide Räder gleich weit in die gleiche Richtung zeigt, wie es bei einer Geradeausfahrt der Fall ist, und einen Anteil $\Delta s_{dreh}$, der bei gleichem Betrag für die Räder unterschiedliche Vorzeichen hat, wie es einer Drehung auf der Stelle entspricht.
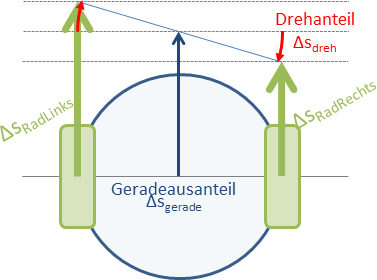
Aus wird direkt ein Ansatz deutlich, der die oben genannten Bedingungen erfüllt: \[\Delta s_{RadLinks}=\Delta s_{gerade}- \Delta s_{dreh}\]
\[\Delta s_{RadRechts}=\Delta s_{gerade}+\Delta s_{dreh}\]
Umgeformt ergibt sich, dass der Geradeausanteil genau dem Mittelwert der von den Rädern gefahrenen Strecken entspricht: \[ \Delta s_{gerade}= \frac{\Delta s_{RadRechts}+\Delta s_{RadLinks}}{2} \] … und der Drehanteil genau der halben Differenz: \[\Delta s_{dreh}= \frac{\Delta s_{RadRechts}-\Delta s_{RadLinks}}{2}\]\
Die Vorzeichen sind so gewählt, dass ein positives $\Delta s_{dreh}$ einer Drehung gegen den Uhrzeigersinn entspricht.
Teil 2: Von Dreh- und Vorwärtsbewegungen zu den aktuellen Koordinaten
Koordinatenveränderungen durch Drehen
Drehungen auf der Stelle verändern nur den Wikel, nicht die Position:
\[\varphi^{i+1}_{Roboter}=\varphi^{i}_{Roboter}+\Delta\varphi^{i}_{Roboter}=\varphi^{i}_{Roboter}+\frac{\Delta s_{dreh}^{i}}{r_{Roboter}}\]
Koordinatenveränderungen durch Vorwärtsfahren
Um zu berechnen, wie sich eine Geradeausfahrt auf die Position des Roboters auswirkt, zeichnen wir uns das Ganze nochmal auf…
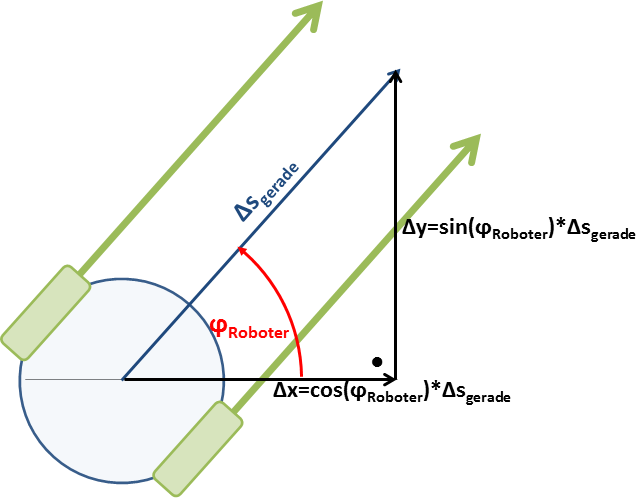
Die Position des Roboters ändert sich also vom Zeitpunkt $t_i$ zum Zeitpunkt $t_{i+1}$ folgendermaßen:
\[p_x^{i+1}=p_x^{i}+cos(\varphi^{i})*\Delta s_{gerade}^{i}\]
\[p_y^{i+1}=p_y^{i}+sin(\varphi^{i})*\Delta s_{gerade}^{i}\]
Zerlegung der Bewegung in kurze gerade Abschnitte
Während sich unser Roboter bewegt, brechnen wir fortlaufend seine aktuelle Position.
Jedes Mal, wenn wir neue Informationen zu den von den beiden Rädern zurückgelegten Strecken haben, berechnen wir daraus eine kleine Drehung und eine kurze Vorwärtsfahrt, deren Auswirkungen wir auf die aktuelle Lage des Roboters addieren.
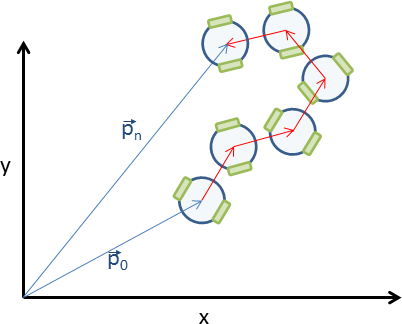
Alles nur eine Näherungslösung
Jedem, der die letzte Skizze aufmerksam angeschaut hat, wird aufgefallen sein, dass es einen Unterschied macht, ob wir bei der Berechnung der zerlegten Bewegung annehmen, dass der Roboter sich zuerst dreht, oder ob er zuerst geradeaus fährt.
Die mir dieser Methode errechneten Positionen sind insofern nur eine Näherungslösung, die im Grenzwert unendlich kleiner Schritte in die exakte Lösung übergeht. Mathematische Methoden zur Abschätzung des bei endlichen Schrittweiten entstehenden Fehlern lernt ihr in einer Numerik-Vorlesung kennen. Für einen kleinen Test mit einfachen Mitteln könnt ihr mal in Processing einen Robotersimulator mit unterschiedlichen Schrittweiten laufen lassen und die Ergebnisse graphisch vergleichen.
