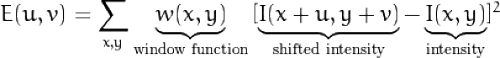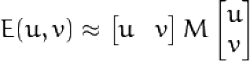Benutzer-Werkzeuge
Seitenleiste
Inhaltsverzeichnis
Interaktives Spiel mit Künstlicher Intelligenz
Einführung
Wer ist dabei?
- Lea Nicolaus
- bis 24.2.2016: Dominic van Deest
Projekidee
Die Idee ist einfach. Ein Computer spielt gegen dich Mühle. Auf dem Tisch liegt das Spielbrett vom Spiel Mühle. Der menschliche Spieler bewegt die Spielsteine per Hand, wobei die Künstliche Intelligenz von oben das Spielbrett beobachtet und seine Anweisungen für die Spielzüge auf dem Display anzeigt. Natürlich soll der Computer nicht leicht zu besiegen sein.
Hilfsmittel
Ausstattung
- Kamera: PS3 Eye Camera
- Stativ
- Spielesammlung
- Computer
Software
- opencv Paket für Python
Links
Open CV http://opencv-python-tutroals.readthedocs.org/en/latest/py_tutorials/py_tutorials.html
Spielidee (zunächst Mini-Mühle, dann Mühle) http://brettspiele.onlinespiele1.com/onlinespiele1_brettspiele_3.htm
Camera Calibration: http://opencv-python-tutroals.readthedocs.org/en/latest/py_tutorials/py_calib3d/py_calibration/py_calibration.html#calibration
Planungsphasen
1. Bildinput verarbeiten
2. Spiel programmieren
3. Dem Computer das Spiel beibringen (KI erstellen)
4. Schnittstellen finden und zusammenfügen
Dokumentation
Phase 1
Kamera und Python
Die Schnitstelle zwischen Python und der Kamera haben wir mit dem Packet „OpenCV“ für Python gefüllt. Das Packet ermöglicht es Bilder von allen angeschlossenen und internen Kameras aufzunehmen, zu betrachten, zu speichern und weiterzuverarbeiten.
Das Packet wird importiert mit import cv2 spielbrett =
Ein Bild Aufnehmen: cv2.VideoCapture(#Kamera)
Die Zählung der Kameras beginnt bei 0 wobei dies meistens die interne Kamera anspricht.
Das aufgenommene Bild wird in eine Variable gelsen:
bild = cv2.VideoCapture(#Kamera).read()
Die variable „bild“ ist ein Tupel, die erste information ist „True“ und die zweite enthällt ein Array mit den Pixeldaten von dem Foto.
Das Bild wird folgendermaßen angezeigt:
cv2.imshow("Anzeige",bild[1])
cv2.waitKey(0)
waitkey ist dafür da, dass gewartet wird, während das Bild angezeigt wird.
Ein Bild Speichern:
cv2.imwrite("Dateiname.png", bild[1])
In Graustufen ändern:
cv2.cvtColor(bild[1], cv2.COLOR_BGR2GRAY)
Ecken im Bild finden
Damit der Computer auch etwas mit dem Bild anfangen kann muss es auf bestimmte Charakteristiker Untersucht werden. Wir haben uns entschieden zunächst die Ecken des Mühle Spielbretts ohne Spielfiguren finden zu lassen, damit es möglich ist ein GRundgerüst zu erstellen, also zu wissen wo die Felder sind.
Dazu verwenden wir Eine Funktion von Open CV: Harris Corner DEtection. corner Harris().
Hinter dieser Funktion steht ein Mathematischer Algorythmus, welche einzelne Regionen (Die größen kann man vorgeben) auf Unterschiede in der Helligkeit. Diese Werden in einem Tupel (u,v)Dargestellt, der folgendermaßen berechnet wird:
Um Ecken aufzuspühren muss diese Fuktion maximiert werden. Die Maximierte Fuktion sieht ungefähr so aus:
wobei
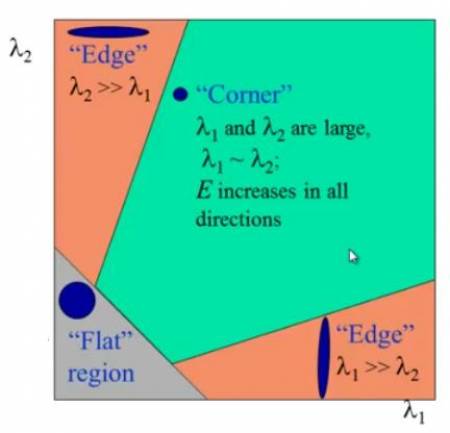
Nun weden die Eigenwerte von M, λ_1 und λ_2 berechnet. Mithilfe dieser Werte kann nun bestimmt werden in welchem Bereich eines Bildausschnitts sich Ecken befinden und wo nicht. Folgende Grafik veranschaulicht dies:
Wir haben in unser Bild von dem Mühlespielbrett einmal alle gefundenen Ecken mit grünen Pixeln eingezeichnet:
Dies ist ein großer Erfolg, denn jetzt ist deutlich wo sich die Felder befinden und somit wo eine Spielfigur sein kann.
Beleuchtung
Die Beleuchtung des Spielbretts erschien uns eine Wichtige Komponente der Bilderkennung, also haben wir verschiedene Belichtungswinkel ausprobiert, um dann festzustellen, dass es nur einen sehr kleinen unterschied macht, wenn man das Brett separat belichtet oder mit der Raumbeleuchtung erhellt. Wichtig ist nur überhapt licht zu haben, so dass nicht zu hohe Kontraste entstehen, die als Ecken gedeutet werden könnten. Die beleuchtung spielte eine größerer Rolle, als wir dasa Bild von dem Brett, zur besseren Ecken Findung über den Schwellwert komplett auf Schwarz oder Weiß gebracht haben. Allerdings hat sich herrausgestellt, dass es besser ist wenn man das Bild in Graustufen betrachtet, um eben diesen Faktor der Beleuchtung auszuklammern.
Zwischzeitliches Abschließen des ersten Projektabschnitts
Da uns einiges Grundwissen aus der Linearen Algebra fehlt unterbrechen wir hier und fahren fort mit dem zweiten Teil des Projekts. Hier offen geblieben sind folgende Fragen:
- Wie kann ich fafür sorgen, dass die Spielfelder als solche identifiziert werden und die einzelnen Positionen als Mittelpunkt der vielen Pixel in der Umgebung abspeicchern?
- Wie erzeuge ich eine Funktion, die ein wenig Toleranz bezüglich der Position und des Kippwinkels der Kamera gibt, sodass die Brettstruktur immer wieder erkannt wird?
- Wie erkenne ich Spielsteine im allgemeinem und wie Unterschiede ich im speziellem die Farbe der Spielsteine (Weiß oder Schwarz)?
Phase 2
Minimühle
Um es ersteinmal für die Kamera und die Rechenkraft des Computers einfach zu halten, entschieden wir uns für die kleine Version der Mühle mit nur 16 Feldern. Dies Musste jetzt samt Spielbrett und Spielregeln virtuell erzeugt werden. Hierbei ist es wichtig in kleinen Arbeitsschritten vorzugehen und nicht alles auf einmal programieren zu wollen, weil man sich dann zu sehr verzettelt, man sollte allerdings das Ziel im Auge behalten.
Ein Spielbrett
Das Spielbrett ist aufgebaut als Array. Jede Liste im Array steht für eine Zeile auf dem Spielbrett und jeder Listeneintrag in dem 'W','S' oder 'x' steht für ein Spielfeld. Die stellen an denen kein Spielfeld ist, sind mit „-“ oder „|“ gekennzeichnet, diese werden nie verändert. Zur verdeutlichung habe ich das bild einer tabelarischen Darstellung des Mühlebretts mit der selben Spielkonstelation wie im Array hinzugefügt.

[['W','-','S','-','W'], ['|','S','W','x','|'], ['S','S',' ','x','x'], ['|','W','x','x','|'], ['S','-','W','-','x']]
Wir haben uns auch alternative Formen des Spielbretts ausgedacht, doch die zuerst genannt stellte sich als am praktisten harraus. Da Das ganze folgende Programm auf dieser Struktur basiert ist es auch nicht einfach diese wieder zu ändern. Alternative Idden waren folgende:
[['A1',' ','A3','00','A5'], ['00','B2','B3','B4','00'], ['C1','C2','00','C3','C4'], ['00','D2','D3','D4','00'], ['E1','00','E3','00','E5']] [[(0,0),'---',(0,2),'---',(0,4)], [' | ',(1,1),(1,2),(1,3),' | '], [(2,0),(2,1),' ',(2,3),(2,4)], [' | ',(3,1),(3,2),(3,3),' | '], [(4,0),'---',(4,2),'---',(4,4)]]
Damit nicht immer ein Array mit viele Klammern und Anführungszeichen zu sehen ist, wenn wir uns das Spielbrett anschauen wollen, gibt es die Funktion zeig_brett, die folgende Ausgabe liefert
def zeige_brett(brett): for i in brett: print " ".join(i)
W - S - W | S W x | S S x x | W x x | S - W - x
def neues_spiel(brett): for x in range(0,5): for y in range(0,5): if brett[x][y] == 'W': brett[x][y] = 'x' elif brett[x][y] == 'S': brett[x][y] = 'x'
Mögliche Züge
Da aus der Spielbrettstruktur kein eindeutiges Schema für erlaubte Züge hervorgeht, muss dies per HAnd eingetrag werden. Die Ideale DAtenstruktur hierfür ist ein Wörterbuch, denn es ordnet einem Feld mehrere andere Felder zu, auf die man von dem ersten Feld aus ziehen kann, falls es frei ist. Dieses Wörterbuch wird später für die findung eines Zugs wichtig werden.
{ (0,0):[(0,2),(2,0) ],
(0,2):[(0,0),(1,2),(0,4)],
(0,4):[(0,2),(2,4) ],
(1,1):[(2,1),(1,2) ],
(1,2):[(1,1),(0,2),(1,3)],
(1,3):[(2,3),(1,2) ],
(2,0):[(0,0),(2,1),(4,0)],
(2,1):[(2,0),(3,1),(1,1)],
(2,3):[(2,4),(1,3),(3,3)],
(2,4):[(0,4),(2,3),(4,4)],
(3,1):[(2,1),(3,2) ],
(3,2):[(3,1),(4,2),(3,3)],
(3,3):[(3,2),(2,3) ],
(4,0):[(2,0),(4,2) ],
(4,2):[(4,0),(3,2),(4,4)],
(4,4):[(4,2),(2,4) ]
} def alle_zuege(farbe, brett):
'''gibt eine Liste für alle möglichen Züge einer Farbe aus'''
startpunkte = []
l =[]
wb = {}
for i in felder_liste(brett, farbe):
if ein_zug(i, brett) != False:
wb.update(ein_zug(i, brett))
return wb
Mühlen
Eine Mühle entsteht genau dann wenn ein Spieler drei Steine seiner Farbe in einer Reihe hat, dafür gibt es in unserem Spielbrett genau 8 verschiedene Möglichkeiten, welche alle in diesem Array festgehalten sind. Hiermit kann überprüft werden ob eine Mühle vorliegt, das tut die untern stehende Funktion pruefe_muele. Diese Funktion greift auf das Array muehlen zu um eine Liste aller Mühlen zu erzeugen die aktuell im Spiel sind.
[[(0,0),(0,2),(0,4)], [(0,0),(2,0),(4,0)], [(0,4),(2,4),(4,4)], [(1,1),(1,2),(1,3)], [(1,1),(2,1),(3,1)], [(1,3),(2,3),(3,3)], [(3,1),(3,2),(3,3)], [(4,0),(4,2),(4,4)]] def pruefe_muehle(farbe, brett): '''gibt die muehlen auf dem aktuellen Feld in einer liste aus''' l=[] for situation in muehlen: feld1 = brett[situation[0][0]][situation[0][1]] feld2 = brett[situation[1][0]][situation[1][1]] feld3 = brett[situation[2][0]][situation[2][1]] if feld1 == feld3 and feld3 == feld2 and feld1 != 'x': l.append(situation) return l
Spielstand
Diese Funktion kann einem sagen auf welchen Feldern gerade schwarze, weiße oder gar keine Figuren sind, dafür muss man für das z ein w, s oder 'x' einsetzen, sofern diese vorher definiert wurden.
def felder_liste(brett, z): ''' gibt eine liste mit allen Spielfeldern in denen z steht''' l=[] for x in range(0,5): for y in range(0,5): if brett[x][y] == z: l.append((x,y)) return l
Die zweite Funktion verät einem den tatsächlichen Spielstand in zahlen, d. h. wie viele Steine einer Farbe sich momentanx auf dem Brett befinden.
def spielstand(farbe, brett):
''' gibt die anzahl von weißen und schwarzen Figuren auf dem spielbrett aus''' k=0 for n in brett: k += n.count(farbe) return k
def wer_ist_am_zug(n, erste_farbe): if (n-1)%2 == 0: return erste_farbe else: if erste_farbe == w: return s else: return w
Das Spiel beginnt: Legephase
Das Spiel geht weiter: Ziehphase
def move_to(start, ziel, farbe, brett): '''bewege einen Spielstein auf ein benachbartes Feld''' brett[start[0]][start[1]]='x' brett[ziel[0]][ziel[1]] = farbe
def ein_zug(position, brett):
'''gibt eine Wörterbuch mit allen tatsächlich möglichen Zügen eines steins von einer bestimmten Position aus'''
wb = {}
l= []
for i in moegliche_zuege[position]:
if i in felder_liste(brett, 'x'):
l.append(i)
wb[position] = (l)
if len(wb) != 0:
return wb
else:
return False
def stein_wegnehmen(farbe, brett): '''gibt eine liste mit allen steinen die nach einem zug weggenommen werden können''' l=[] for i in moegliche_zuege: if brett[i[0]][i[1]] != farbe and brett[i[0]][i[1]] != 'x': if i not in sum(pruefe_muehle(farbe, brett),[]): l.append(i) return l
def ziehen(brett, farbe): '''sucht den besten Zug für eine der farben und führt ihn aus''' if len(alle_zuege(farbe, brett)) == 0: print str(farbe)+' hat verloren' else: start= random.choice(alle_zuege(farbe, brett).keys()) ziel = random.choice(alle_zuege(farbe, brett)[start]) move_to(start, ziel, farbe, brett)
def wegnehmen(vor_zug, nach_zug, brett, am_zug): if vor_zug != nach_zug and len(nach_zug)>= len(vor_zug): stein = random.choice(stein_wegnehmen(am_zug, brett)) brett[stein[0]][stein[1]] = 'x' print str(am_zug) +' hat einen Stein weggenommen'
Spielend
def spielende(brett): '''Der Gewinner wird zurückgegeben''' if len(alle_zuege(w, brett)) == 0 or spielstand(w, brett) <= 2: return s if len(alle_zuege(s, brett)) == 0 or spielstand(s, brett) <= 2: return w
Funktion für einen Zufälligen speilverlauf
Steine setzen
def steine_setzen(farbe, brett): neues_spiel(brett) n=0 while n<=11: n= n+1 am_zug = wer_ist_am_zug(n, farbe) vor_zug = pruefe_muehle(am_zug, brett) feld = random.choice(felder_liste(brett, 'x')) brett[feld[0]][feld[1]] = am_zug nach_zug = pruefe_muehle(am_zug,brett) print str(am_zug)+' setzt:' zeige_brett(brett) print'_________________' if wegnehmen(vor_zug, nach_zug, brett, am_zug) == True: zeige_brett(brett) print '__________'
n=0 print 'Setzen:' steine_setzen(w,spielbrett) print 'Spielstart:'
while True: if n == 0: zeige_brett(spielbrett) n=n+1 am_zug = wer_ist_am_zug(n,w) print '____________________' print str(am_zug) +' zieht:' vor_zug = pruefe_muehle(am_zug, spielbrett) ziehen(spielbrett, am_zug) nach_zug = pruefe_muehle(am_zug,spielbrett) wegnehmen(vor_zug, nach_zug, spielbrett, am_zug) zeige_brett(spielbrett) if spielende(spielbrett) != None: print 'spiel ist vorbei' print n break