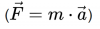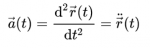Mathesis Wiki

Das Projektziel ist, eine Engine zu bauen, welche die (gravitationsbedingte) Interaktion mehrerer Himmelskörper dreidimensional darstellt.

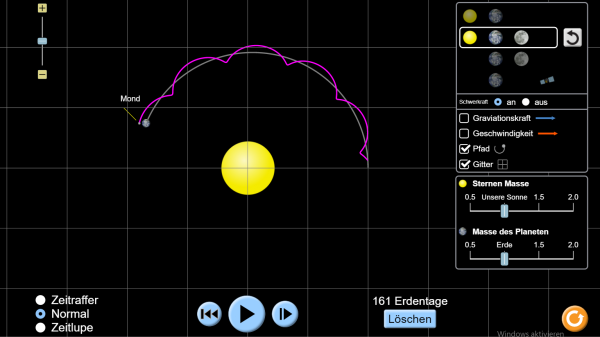
• Beispiel aus dem Internet: https://phet.colorado.edu/sims/html/gravity-and-orbits/latest/gravity-and-orbits_de.html

Dabei haben wir zuerst ein vereinfachtes 2-D-Programm, basierend auf den Kepler'schen Bahngleichungen, und anschließend eine verbesserte Version, welche mit den Newton'schen Gleichungen rechnet, erstellt.

• Theodor Weichler - 409444
• Alex Sakritz - 414218
• Awid Gabanski - 409334
• Selin

Die Grundidee des Programmes ist folgende - dem Programm werden für jeden Himmelskörper/Planeten gewisse Startparameter übergeben (Darunter am wichtigsten: die Position). Welche Parameter gebraucht werden hängt von der jeweiligen Methode ab. Das Programm berechnet dann daraus die neue Position der jeweiligen Körper, wobei sich dabei unter Umständen die Parameter ändern. Rechnet das Programm nun weiter, so „updatet“ sich die Position der einzelnen Körper annähernd stetig und ein himmelsmechanisches Bewegungssystem wurde simuliert.

Unser erster Ansatz war eine Berechnung mit Hilfe der Kepler'schen Bahngleichung:

$E ~=~ M ~-~ e·sin(E)$

Dabei stehen die Variablen $E$ und $M$ für die Exzentrische bzw. die Mittlere Anomalie, zwei zu berechnende Zwischenwerte, und die Variable $e$ für die Exzentrizität, unseren ersten Bahnparameter.

Die Kepler'schen Bahnparameter sind: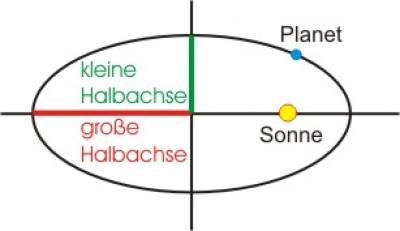

• $a$ - die große Halbachse

• $e$ - die Exzentrizität

• $ω$ - die Winkelgeschwindigkeit

Die große Halbachse bezeichnet hierbei die Hälfte des größten Durchmessers einer Ellipse, welcher zudem in jedem Fall durch die beiden Brennpunkte führt.

Die Exzentrizität hingegen ist umgangssprachlich als die Stauchung einer sonstigen Kreisbahn zu verstehen, sie ergibt sich aus einem Verhältnis der großen und kleinen Halbachse (Hälfte des kleinsten Durchmessers).

class Body:     #planet/trabant

def __init__(self, name, radius, position, winkelgeschwindigkeit, exzentrizitaet, grossehalbachse, objekt):
	
	self.name = name
	self.rad = radius
	self.pos = position
	self.angularv = winkelgeschwindigkeit #mean angular velocity
	self.ecc = exzentrizitaet
	self.axis = grossehalbachse
	self.ob = objekt
      
      # a: Große Halbachse
      # ε: Exzentrizität
      # ω: Winkelgeschwindigkeit

Die übrigen angegebenen Werte sind

• der Name (zur Benennung im Programm)
• der Radius (zur Darstellung im Programm)
• die Position (als erste Ortsangabe, wird vom Programm geupdatet)
• das „Objekt“ (hier wird der Körper als VisualPythonSphere gespeichert)

Mit unseren drei Anfangsparametern und der Variable $t$, der fortschreitenden Zeit, lässt sich nun mit Hilfe von drei Winkeln eine neue Position errechnen, dafür werden folgende Gleichungen nacheinander gelößt:

• $M$ - Mittlere Anomalie: $$M ~=~ ω·t$$

• $E$ - Exzentrische Anomalie: $$E ~=~ M ~-~ e·sin(E)$$

• $θ$ - Wahre (True) Anomalie: $$tan(\frac{θ}{2}) ~=~ \sqrt{\frac{1+e}{1-e}}·tan(\frac{E}{2})$$

• $r$ - Position als Abstand zum Mittelpunkt (in Polarkoordinaten mit Wahrer Anomalie): $$r ~=~ \frac{a·(1-e²)}{1+e·cos(θ)}$$

def update(self, Tges, scale = 50): #Tges in Seconds
	for i in range(len(self.himmelskoerper_liste)):
		e, v, a = self.himmelskoerper_liste[i].ecc, self.himmelskoerper_liste[i].angularv, self.himmelskoerper_liste[i].axis
		M = v * Tges # M = mean anomaly		
		
		def f(x):
			return x-e*math.sin(x)-M #Kepler Equation
		def f1(x):
			return 1-e*math.cos(x) #derivative of Kepler Equation
			
		E = InverseKepler(f, f1, 1) # E = eccentric anomaly
		θ = 2*math.atan(math.sqrt((1+e)/(1-e))*math.tan(E/2)) # θ = real anomaly
		r = (a*(1-e**2))/(1+e*math.cos(θ)) # r = euclidean distance to center object
		
		self.himmelskoerper_liste[i].ob.pos = r*vpy.vector(math.cos(θ), math.sin(θ), 0)

Besonders problematisch ist dabei die sogenannte Kepler-Gleichung, $$E ~=~ M ~-~ e·sin(E)$$

welche als transzendente Gleichung nicht analytisch lösbar ist und deswegen mit Hilfe eines Annäherungsverfahrens gelöst werden muss.

Als einfachste Lösung haben wir das Newton-Verfahren benutzt, welches mit Hilfe der 1. Ableitung eine schrittweise immer nähere Approximation liefert:

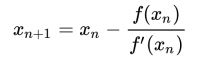
Als Schrittweite haben wir uns nach zahlreichem Herumprobieren für fünf Iterationen entschieden:

def InverseKepler(f, f1, x0, d=5): #general Newton-Method for non-linear equations, used specifically to solve the Kepler-Equation with f1 = f' = df/dx ∀x	for i in range(d):
	x0 = x0-(f(x0)/f1(x0))
return x0

Damit wäre die erste Version des Programmes abgeschlossen. Die drei bisher von uns gewählten Parameter (große Halbachse, Exzentrizität und Winkelgeschwindigkeit) birgen den Nachteil, dass alle Werte zunächst empirisch erhoben werden müssen, das Programm selbst rechnet also nicht mit Gravitation, sondern lediglich mit den von uns beobachteten Parametern für elliptische Bewegung. Dadurch ist es nicht auf beliebige Himmelskörper anzuwenden, in diesem spezifischen Fall an zwei Dimensionen gebunden und alles in Allem nur als Prototyp zu betrachten.

Unser eigentliches Programm funktioniert analog zu der oben beschriebenen Methode, einzig die zu übergebenen Bahnparameter und entsprechend zu berechnenden Gleichungen unterscheiden sich.

Die für einen Gravitationsansatz relevanten Parameter sind:

• $\vec v$ - die Geschwindigkeit und die entsprechenden Beschleunigungen $\vec a$
• $m$ - die Masse des Himmelskörpers

class Body:     #planet/trabant

def __init__(self, name, radius, masse, position, objekt):
	
        self.name = name
	self.rad = radius
	self.mass = masse
	self.pos = position
	self.v = geschwindigkeit
	self.ob = objekt
      
      #name, masse[kg], radius[m], position/anfangs der Abstand zur Sonne[m]
    

Die restlichen vier Werte bleiben wie gehabt. Als erste Gleichung ziehen wir uns nun das zweite Newton'sche Gesetz her:

wobei gilt:

Setzt man nun diese Kraft mit der Newton'schen Gravitationskraft gleich,

$$m_{1}·\ddot{\vec r}(t) ~=~ \vec F ~=~ G·\frac{m_{1}·m_{2}}{\vec r(t)²}$$

hätte man eigentlich nur noch diese Gleichung zu lösen, um einen neuen Positionswert zu ermitteln. Die einzige Schwierigkeit liegt dabei, dass diese Gleichung ein Zweikörperproblem behandelt. Da wir in unseren Szenarien jedoch n-viele Körper simulieren können wollen, erweitert sich diese Gleichung (wohlgemerkt für jeden einzelnen Körper separat):

$$\ddot{\vec r}(t) ~=~ G·(\frac{m_{2}}{\vec r_{1-2}(t)²}+\frac{m_{3}}{\vec r_{1-3}(t)²}+\frac{m_{4}}{\vec r_{1-4}(t)²}+\ldots+\frac{m_{n}}{\vec r_{1-n}(t)²})$$

Diese Gleichung ist für $n ≥ 3$ nicht mehr so leicht analytisch lösbar, weswegen wieder ein Approximationsverfahren eingesetzt werden muss. Im Code sieht die Rechnung wiefolgt aus:

def update(self):
	G = 6.67430E-11 #gravity constant
	M, X = [], [] #M = list of masses, X = list of positions
	
	for i in range(len(self.himmelskoerper_liste)):
		M.append(self.himmelskoerper_liste[i].mass)
		X.append(self.himmelskoerper_liste[i].ob.pos)
	
	for i in range(len(self.himmelskoerper_liste)):
		a = vpy.vector(0,0,0)	 #a = acceleration
		
		for j in range(1,len(self.himmelskoerper_liste)):
			i2 = (i+j) % len(self.himmelskoerper_liste)
			a += G * M[i2]*(X[i2]-X[i])*1/(((X[i2]-X[i]).mag**3))
		
		#print(X[i], self.himmelskoerper_liste[i].v)
		#print(leapfrog(X[i], self.himmelskoerper_liste[i].v, a))
		self.himmelskoerper_liste[i].ob.pos = leapfrog(X[i], self.himmelskoerper_liste[i].v, a)[0]
		self.himmelskoerper_liste[i].v = leapfrog(X[i], self.himmelskoerper_liste[i].v, a)[1]

Wir haben uns für das sogenannte Leapfrog-Verfahren entschieden, welches zum numerischen Lösen von Differentialgleichungen eben dieses Typus ($\ddot{x} ~=~ \dot{v} ~=~ a(x)$) verwendet wird.

Dabei vollzieht das Leapfrog-Verfahren anders als das herkömmliche Explizite-Euler-Verfahren bei jedem Schritt mit Hilfe der zweiten Ableitung eine prognostische Zwischenrechnung (es „leapt“ sozusagen einen halben Schritt in die Zukunft), wodurch es eine genauere Approximation bietet.

def leapfrog(x0, v0, a, dt = 60): #dt sets the time intervall per iteration (in seconds)
    v0 = v0 + a*dt*1/2
    x0 = x0 + v0*dt
    v0 = v0 + a*dt
    return x0, v0      

Damit lässt sich nun die Position jedes einzelnen Körpers ermitteln und unsere Gravitationsengine ist gebaut. Diese benötigt im Vergleich zum Ansatz mit der Keplergleichung lediglich die Körpermassen $m$, die Ausgangsgeschwindigkeiten $\vec v$ und natürlich die Ausgangsposition $\vec r$.

Der Radius wird in der Rechnung selbst nicht berücksichtigt, da die Newton'schen Modelle vereinfacht von Punktmassen ausgehen. Weiterhin werden Relativistische Effekte nicht berücksichtigt, was zwar in der überwiegenden Mehrheit der Fälle vernachlässigbar ist, aber beispielsweise im bekannten Falle der Anomalie des Merkur-Perihels zu Unstimmigkeiten führen kann.

»Die restlichen Links und Seiten:

Wochen-Protokolle

Sourcecode

Quellen