Die initiale Idee war die, eines digitalen Notizbuches für Melodien. Eine, optimaler Weise auch für mobile Endgeräte entwickelte, Applikation, die über das Mikrofon eingesungene, -gesummte, -gepfiffene oder mit einem Instrument -gespielte Phrasen direkt in musikalische Noten übersetzt und diese sowohl als Partitur, als auch als MIDI-File ausgibt.

Während eingangs von einem überschaubaren Algorithmus ausgegangen wurde, der in der Lage ist eine ganz bestimmte Art von Ton/Instrument, wie z.B. Pfeifen, in einer möglichst ruhigen Umgebung erfassen kann. Das heißt nur ein monophones Signal eines einzigen Timbres (s. Timbre, \ref{sec_timbre}).

Im Prozess der Signalanalyse charakterisierte sich jedoch schnell heraus, dass die Qualität eines musikalischen Signals von einer Vielzahl von Faktoren abhängig ist. Raum, Umgebungsgeräusche, Anschlag des Tones, Instrument/Stimme, Mikrofon und natürlich insbesondere die Tonhöhe selbst verändern die Qualität des zu Hörenden immens. Auf Grundlage dieser Erkenntnis wäre es sicherlich möglich gewesen einen sehr speziellen Alogrithmus zu schreiben, der mit relativ einfachen Verarbeitungsschritten für ein klar umgrenztes Anwendungsfeld ein zufriedenstellendes Ergebnis liefert. Sobald jedoch ein einziger Parameter variiert wird, wäre ein solches Verfahren nicht mehr erfolgversprechend. Gemessen an der Grundidee Musikern ein Tool an die Hand zu geben, mit dem sie unterwegs bzw. spontan Ideen festhalten zu können wäre so eine unflexible Lösung ein ernüchterndes Ergebnis.

So entwickelte sich der „einfache“ Tonhöhenerkennungsalogrithmus sukzessive zu einem Experimentierbaukasten, in dem über eine Vielzahl von Parametern und verschiedensten Filtern- und Masken versucht wird eine möglichst allgemeingültige Erkennung von Grundtönen in einem komplexen Tonbild zu erreichen.

Als Referenz und Messlatte diente uns in erster Linie das im Bereich der Musikproduktion etablierte Celemony Melodyne. Melodyne ist in seinem Kern ein Werkzeug zur Tonkorrektur (Höhe, Länge, Amplitude, Modulation). Das Herzstück von Melodyne ist dabei ein effizienter Alogrithmus, der (inzwischen sogar polyphon) das Eingangssignal zerlegt, zusammenhängende Töne und ihre spektralen Anteile erkennt und diese über einer Pianoroll zur Bearbeitungen abbildet. Der Quellcode dieses und ähnlicher Produkte ist jedoch leider nicht frei zugänglich.

Im Zuge des Prozesses wurde eine Vielzahl von Manipulationsverfahren auf den Datensatz angewandt um die optimale Prozesskette gegen eine Reihe von Samplen zu erproben. Dabei wurden immer neue Aspekte des Datensatzes sichtbar, welche immer neue Anpassungen erforderten. So wurde zum Beispiel inital davon ausgegangen, dass es sinnvoll wäre das Eingangssignal zunächst in jedem Fall in ein Monosignal umzuwandeln und alle Amplituden nur als Beträge abzubilden. Am der Entwicklungskette stellte sich jedoch heraus, dass die Phasenverschiebung, Interferenz und Auslöschungen so in nicht kalkulierbaren Fehlern münden. Auch die Analyse unterschiedlicher Instrumentensamples zur Bildung einer Datenbank von Vergleichstimbres wurde vorgenommen im späteren Verlauf implementiert.

Zum Zeitpunkt dieser Dokumentation steht ein Algorithmus, welcher nach wie vor einen langen Weg zu gehen hat um die an ihn gestellten Anforderungen vollends zu erfüllen. Während einige Samples und Laute sich gut erfassen und einem Instrument aus der Datenbank zuordnen lassen, führen andere zu weit weniger aussagekräftigen Ergebnissen, sei es aufgrund von Polyphonie, Auslöschungen oder des inkonstanten Timbres (z.B. menschliche Stimme). Interessant ist dabei, dass sich die Problemfälle ebenso in Melodyne als kritisch herausstellen, weshalb davon ausgegangen werden kann, dass der Lösungsalgorithmus ähnliche Leitsätzen folgt. Aufgabe für die Zukunft ist es, die Zuverlässigkeit des Algorithmus und die Rechenzeit zu optimieren, die Timbrebibliothek auszubauen, die Anwendung für weitere Plattformen aufzubereiten (Webapplikation, Android, evtl. VST) und in diesem Zuge ein zugängliches UI zu entwickeln.

Wie eingangs bereits beschrieben muss ein eindimensionales WAV-Eingangssignal zerlegt und so aufbereitet werden, dass sich für jeden Zeitpunkt die Grundfrequenz(en) des gespielten Tons bzw. der gespielten Töne ermitteln lässt. Im folgenden müssen Anfangs- und Ausstiegsbedingung für jeden zusammenhängenden Ton ermittelt werden und so die Gesamtlänge einer Note in über $t$ (in [samples] oder [s]) bestimmt werden. Über diese Länge wird nun eine gemittelte Frequenz $f_\mathrm{mean}$ errechnet und diese einem Ton in der chromatischen Skala zugeordnet. Die gefunden $t$-Werte der Töne wiederum müssen in musikalische Notenwerte umgerechnet werden. Dies geschiet über ihre relative Längen. Die Ausgabe als Notenblatt und MIDI kann über die Python-Bibliothek \textit{music21} erfolgen.

\label{loesung} Die Lösungsstruktur ist in drei Hauptschritte untergliedert.

• Transformation zum Spektrogramm

• Harmonische Mustererkennung und Ermittlung potentieller Fundamentalfrequenzen

• Zerlegung in diskrete Noten

Der Inputsound ist in der Darstellung \begin{align*} y&= \begin{bmatrix} y_1 & y_2 & \cdots & y_{\tilde{m}-1} & y_{\tilde{m}} \end{bmatrix}\\ y_{j}&,\quad j\in[1,\tilde{m}] \end{align*} geladen und hat die Sampelrate $f_s$, auf Deutsch Abtastfrequenz, zugeordnet. Dieser wird in \textquotedblleft Sections\textquotedblright unterteilt und in einer Matrix $\hat{y}_s$ neu angeordnet. Die Spalten von $\hat{y}_s$ sollen einem Zeitintervall von $\frac{1}{s}$ entsprechen. $s$ ist die Section-frequenz, in die der Sound $y$ zerlegt werden soll. Somit besitzt die die Matrix $y_s$ die Dimension $\hat{n}\times m$ mit $\hat{n} = \frac{f_s}{s}$ und $ m = \frac{\tilde{m}s}{f_s}$. \begin{align*} \hat{y}_s&= \begin{bmatrix} y_1 & y_{\hat{n}+1} & \cdots & y_{\hat{n}(m-2)+1} & y_{\hat{n}(m-1)+1}\\ y_2 & y_{\hat{n}+2} & \cdots & y_{\hat{n}(m-2)+2} & y_{\hat{n}(m-1)+2}\\ \vdots & \vdots & \ddots & \vdots & \vdots\\ y_{\hat{n}-1} & y_{2\hat{n}-1} & \cdots & y_{\hat{n}(m-1)-1} & y_{\hat{n}m-1}\\ y_{\hat{n}} & y_{2\hat{n}} & \cdots & y_{\hat{n}(m-1)} & y_{\hat{n}m} \end{bmatrix}\\ \hat{y}_{s,jk}&=y_{j+(\hat{n}-1)k},\quad j\in[1,\hat{n}],\quad k\in [1,m] \end{align*}

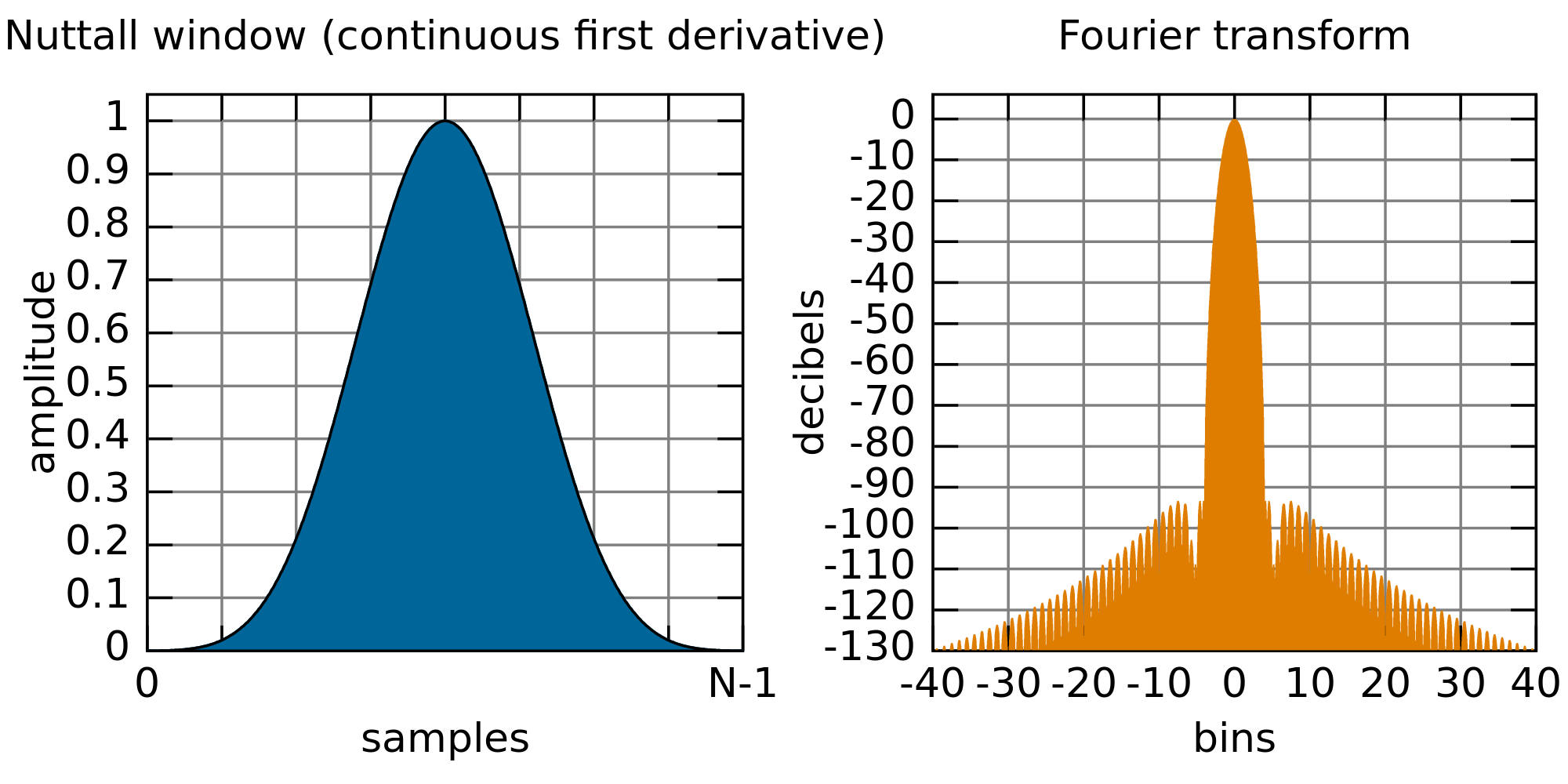
Um in der späteren Fouriertransformation möglichst wenig hochfrequente Störanteil, die durch das Sectioning hervorgerufen werden, zu minimieren, werden sogenannte \textquotedblleft Windowfunctions\textquotedblright verwendet. Da diese Informationen an den Rändern weniger gewichten, wie das von uns gewählte \textquotedblleft Nuttall\textquotedblright -Fenster $f(k)$, Abbildung \ref{nuttall}, wird eine Section mit ihrem Vorgänger und der folgenden Section erweitert, um eine möglichst große Gewichtung der eigentlichen Section zu erhalten.

Somit entsteht die Matrix $\tilde{y}_s$ der Dimension $\tilde{n}\times m$ mit $\tilde{n}=3\hat{n}$ in folgender Form: \begin{align*} \text{mit:}\quad W&=\begin{bmatrix} f(1) & 0 & \cdots & 0 & 0\\ 0 & f(2) & \cdots & 0 & 0\\ \vdots & \vdots & \ddots & \vdots & \vdots\\ 0 & 0 & \cdots & f(\tilde{n}-1) & 0\\ 0 & 0 & \cdots & 0 & f(\tilde{n}) \end{bmatrix}\\ \tilde{y}_s&=W \cdot \begin{bmatrix} 0 & y_1 & \cdots & y_{\hat{n}(m-3)+1} & y_{\hat{n}(m-2)+1}\\ 0 & y_2 & \cdots & y_{\hat{n}(m-3)+2} & y_{\hat{n}(m-2)+2}\\ \vdots & \vdots & \ddots & \vdots & \vdots\\ y_{2\hat{n}-1} & y_{3\hat{n}-1} & \cdots & y_{\hat{n}m-1} & 0\\ y_{2\hat{n}} & y_{3\hat{n}} & \cdots & y_{\hat{n}m} & 0 \end{bmatrix}\\ \tilde{y}_{s,jk}&=\begin{cases} \text{wenn } j+(k-2)\hat{n} < 1:& 0\\ \text{wenn } j+(k-2)\hat{n} > \tilde{m}:& 0\\ \text{sonst: }& f(j)\cdot y_{j+(k-2)\hat{n}} \end{cases}\\ \text{mit: }&\quad j\in [1,\tilde{n}],\quad k\in[1,m] \end{align*} Nun werden unten an $\tilde{y}_s$ Nullen angefügt. Dies wird \textquotedblleft Zeropadding\textquotedblright genannt und sorgt für eine harmonisch interpoliertes Spektrum. Dieses wird gebraucht um später größere Genauigkeit im Frequenzbereich in der Harmoniefilterung zu erlangen. Somit erhalten wir $y_s$ als fertig vorbereitete Stufe vor der Fouriertransformation. Im Programm kann die Anzahl der Nullen wird mit einem Parameter $z_p\ge 0$ vorgegeben. Die so entstehende Matrix hat die Dimension $\tilde{n}(1+z_p)\times m$. \begin{align*} y_s&= \begin{bmatrix} 0 & f(1)y_1 & \cdots & f(1)y_{\hat{n}(m-3)+1} & f(1)y_{\hat{n}(m-2)+1}\\ 0 & f(2)y_2 & \cdots & f(2)y_{\hat{n}(m-3)+2} & f(2)y_{\hat{n}(m-2)+2}\\ \vdots & \vdots & \ddots & \vdots & \vdots\\ 0 & 0 & \cdots & 0 & 0\\ 0 & 0 & \cdots & 0 & 0 \end{bmatrix}\\ y_{s,jk}&=\begin{cases} \text{wenn } \tilde{n}<j:&0\\ \text{sonst: }&\tilde{y}_{s,jk} \end{cases},\quad j\in [1,\tilde{n}(1+z_p)],\quad k\in[1,m] \end{align*}

Nun wird jede Section, also jede Spalte von $y_s$, mittels eines \textquotedblleft Fast Fourier Transform\textquotedblright-Algorithmus, kurz FFT genannt, Fouriertransformiert. Da $y_s$ reell ist, ist die komplexe FFT der Spalten von $y_s$ komplex-konjugiert-y-achsenssymetrisch. Somit können negative Frequenzen ignoriert werden da sie die gleiche Information beinhalten. Somit bekommt entsteht eine komplexe Matrix $Y$ mit der Dimension $n\times m$ mit $n=\frac{\tilde{n}(1+z_p)}{2}$. Falls $n$ eine nicht ganze Zahl ist wird sie zur nächsten ganzen Zahl aufgerundet. Die dazu gehörige diskrete Frequenzachse ist $f$ \begin{align*} f&=\begin{bmatrix} 0 & \frac{f_s}{2(n-1)} & \frac{2f_s}{2(n-1)} & \cdots & \frac{(n-3)f_s}{2(n-1)} & \frac{(n-2)f_s}{2(n-1)} & f_s \end{bmatrix}\\ f_j&=f_s\frac{j-1}{2(n-1)},\quad j\in [1,n] \end{align*} und die Zeitachse $t$. \begin{align*} t&=\begin{bmatrix} 0 & \frac{1}{s} & \frac{2}{s} & \cdots & \frac{m-2}{s} & \frac{m-1}{s} \end{bmatrix}\\ t_k&=\frac{k-1}{s},\quad k\in [1,m] \end{align*} Da hier die Phase nicht so wichtig ist wie der Betrag von $Y$ wird der Betrag genommen um $Y_{\text{abs}}=\sqrt{Y\cdot\bar{Y}}$ zu erhalten. Die grafische Visualisierung heißt Spektrogramm. In Abbildung \ref{spektrum} ist solch eins dargestellt.

Um potentielle fundamental Frequenzen zu heraus zu filtern, wird das Spektrum mit einer Harmoniemaske korreliert um so Peaks hervorzuheben, welche idealerweise die Grundfrequenz einer harmonischen Serie sind. Der Korrelationstensor $C$ ist dabei von 3 Parametern abhängig und besitzt die Dimension $n\times \xi \times m$ mit $\xi=\frac{n}{h}$ abgerundet zur nächsten ganzen Zahl. $h$ ist die Anzahl der einbezogenen Obertöne. $a$ ist der Obertonabfallkoeffizient. \begin{align*} C_{k=1}&=\begin{bmatrix} 0 & 0 & \cdots & 0 & \frac{1}{1+a(\xi-1)}\\ 0 & 0 & \cdots & 0 & 0\\ \vdots & \vdots & \ddots & \vdots & \vdots\\ \frac{1}{1+a} & 1 & \cdots & 0 & 0\\ 1 & 0 & \cdots & 0 & 0 \end{bmatrix}\\ C_{jlk}&=\begin{cases} \text{wenn }j>l\cdot\xi:&0\\ \text{wenn }j\mod l\ne 0:&0\\ \text{sonst: }&\frac{1}{1+a(\frac{j}{l}-1)} \end{cases}\\ \text{mit:}&\quad j\in [1,n],\quad k\in [1,m],\quad l\in [1,\xi] \end{align*} Mit dem Korrelationstensor $C$ kann nun das korrelierte Spektrogramm $\tilde{Y}_C$ erstellt werden. In folge des Overlappings und Zeropaddings müssen mindestens die ersten $3z_p$ Frequenzen entfernt werden beziehungsweise zu $0$ gesetzt werden. \begin{align*} \tilde{Y}_{C,lk}&=\sum_{j} C_{jlk}\cdot Y_{\text{abs},jk}\\ Y_{C,lk}&=\begin{cases} \text{wenn }l<6z_p:&0\\ \text{sonst: }&\tilde{Y}_{C,lk} \end{cases} \end{align*} In dieser Form werden lokale Maxima gesucht und die $p$ größten gespeichert. $Y_C$ kann als Farbplot gezeichnet werden. Die zugehörigen Amplituden zu den Maxima werden in Abbildung \ref{convthat}

ploty.pdf

Die Maxima werden in \texttt{pitchc}, die Frequenz des Maximums, in \texttt{ampli}, die Lautstärke des gesamten Tones (mit Obertönen), und \texttt{index}, der zur Frequenz zugehörigen Indexes, abgespeichert. Diese haben jeweils die Dimension $p\times m$. Dabei ist $p$ die Anzahl der größten lokalen Maxima in in Frequenzrichtung.

Da die quasi Korrelation zwar hinweise auf Fundamentalfrequenzen gibt, vor allem wenn die Fundamentalfrequenz nicht die lauteste ist, kann sie nicht zwischen Überlagerung von Obertönen differenzieren. Falls die Obertöne von verschiedene Tönen sich überlagern, wovon in harmonischer Musik ausgegangen wird, werden diese fälschlicherweise mit Hintergrundrauschen addiert. Um dies zu differenzieren, werden die Punkte im Spektrum, welche Obertöne der potentiellen Fundamentalfrequenzen sind, approximativ in Beispiel-Obertonverteilungen zerlegt. Dies wird nicht mit einem linearen Least-Square-Alogrithmus sondern mit einem Least-Absolute-Algorithmus gelöst um den Einfluss von Ausreißern zu verkleinern. Es wird ein Vektor $b$ definiert, welcher die Amplituden der Punkte der potentiellen Fundamentalfrequenzen und deren Obertöne vereint. Die Matrix $A$ beinhaltet in Spalten die normierten Obertonverteilungen, sodass diese passend auf $b$ abbilden. Die letzte Spalte in $A$ besteht aus einem normierten Einservektor, welcher einen Offset darstellt und Rauschen filtern soll. Der Vektor $x$ ist damit in der folgenden Gleichung die Lautstärke der einzelnen Obertonverteilungen.

\begin{align*} A\cdot x&\approx b\quad\text{mit: }x\in\mathbb{R}^n_+\\ \min\limits_x \|A\cdot x -b\|_{1}&=\|A\cdot x -b\|_{1} \end{align*} $\|\cdot\|_p$ ist dabei die $p$-Norm.

\texttt{ampli} wird nun als Summe der Obertonverteilungsgewichtung für eine potenzielle Fundamentalfrequenz berechnet. Somit sollen Frequenzen welche nicht in die Obertonverteilung passen eine möglichst kleine Amplitude haben und die Amplituden der Frequenzen, welche wirkliche Fundamentalfrequenzen sind, mit der Tonlautstärke korrelieren. Die Obertonverteilungen werden entweder mit Funktionen wie zum Beispiel $f(k)=\frac{1}{1+(a(k-1)^b)}$, mit dem $k$-ten vielfachen der Grundfrequenz, oder durch eine Obertonanalyse von verschiedenen Samples vorgeben.

Als Ausgangspunkt für die Notenbestimmung liegen \texttt{pitchc} und \texttt{ampli} zu Grunde. Eine typische Note besitzt einen Anschlag, eine Ausklingzeit und eine Tonhöhe. Der Anschlag ist durch einen starken Anstieg in \texttt{ampli} charakterisiert. Die Ausklingzeit ist durch das Abfallen von \texttt{ampli} unter einen bestimmten Schwellwert definiert. Dieser Schwellwert steht im Verhältnis zur maximalen Lautstärke des Tones. Die Tonhöhe darf keine zu großen Schwankungen haben um als zusammenhängender Ton zu gelten. Somit können für die Maximumslinien Bedingungen aufgestellt werden welche den Anfang und das Ende eines Tones bestimmen. In folgenden wird $A(t)\hat{=}\texttt{ampli}$ als Stärke einer Maximumslinie und $F(t)\hat{=}\texttt{pitchc}$ als Fundamentalfrequenz als analytisches Analogon verwendet. $t_{\text{start}}$ und $t_{\text{end}}$ markieren Start und Endzeitpunkt. Dabei ist $K(x,a)$ der Glättungskern welcher die Notenhäufigkeit verringert. Die Breite des Kerns muss dabei so gewählt werden das Häufigkeit und Länge der Noten in etwa der gängiger Musik entsprechen. \begin{align*} \text{mit:}\quad K(x,a)&=\begin{cases} \text{falls } \left|\frac{t}{a}\right|<1:& \big(1-|\frac{x}{a}|\big)^2\\ \text{sonst} :&0 \end{cases}\\ x \in \mathbb{R},\quad a\in\left]0,\infty\right[\\ \frac{\mathrm{d}^2}{\mathrm{d}x^2}\big(K(t,a_1)\ast_t A(t)\big)(t_{\text{start}})&=0\quad\cap\\ \frac{\mathrm{d}}{\mathrm{d}x}\big(K(t,a_1)\ast_t A(t)\big)(t_{\text{start}})&>0\quad\cap\\ \left|\frac{\mathrm{d}}{\mathrm{d}x}\big(K(t,a_2)\ast_t F(t)\big)(t_\text{start})\right|&<b\\ \frac{\big(K(t,a_1)\ast_t A(t)\big)(t_{\text{end}})}{\max\limits_t{\big(K(t,a_1)\ast_t A(t)\big)}}&<c\quad\cup\quad \left|\frac{\mathrm{d}}{\mathrm{d}x}\big(K(t,a_2)\ast_t F(t)\big)(t_\text{end})\right|&>b\\ a_1,a_2,b,c\in\left]0,\infty\right[,\quad t\in\mathbb{R} \end{align*}

Die Bereiche zwischen $t_{\text{start}}$ und $t_{\text{end}}$ werden in \texttt{note} als Boolean für die Sections abgespeichert. Die Notenfrequenz $P$ wird innerhalb der Note mit einer robusten Regression \begin{align*} \min\limits_P\int_{t_{\text{start}}}^{t_{\text{end}}}\arctan\Big[c\big(F(t)-P\big)^2\Big]\,\mathrm{d}t=\int_{t_{\text{start}}}^{t_{\text{end}}}\arctan\Big[c\big(F(t)-P\big)^2\Big]\,\mathrm{d}t\\ \end{align*} oder mit dem arithmetischen Mittel \begin{align*} P=\frac{1}{t_{\text{end}}-t_{\text{end}}}\int^{t_{\text{end}}}_{t_{\text{start}}}F(t)\,\mathrm{d}x \end{align*} bestimmt.

Die entwickelte Verarbeitungskette sieht dabei wie folgt aus:

\paragraph{Main.py:} Inputaufforderung, Ansteuerung der Einzelfunktionen, Ausgabe via \textit{matplotlib} zu Verifizierung, Übergabe an \textit{music21} zur Endausgabe an ein Notensatzprogramm (z.B. \textit{MuseScore2.0}) und Ablage als *.xml-File.

Importiert Sampler.py, SigPro.py, Convthat.py, Notefinder.py

\paragraph{Sampler.py:} Input des Soundfiles, entweder Übergabe von bestehenden *.wav-Dateien an ein numpy-Array oder Schreiben eines 1D-Arrays mit der vorgegebenen Samplerate (44100 Hz) bis die Ausstiegsbedingung (Drücken der Enter-Taste) erreicht ist, im Zweifel Stereo-to-Mono-Konvertierung, Ausgabe über die Soundkarte

\paragraph{SigPro.py:} Aufbereitung des Datensatzes für die Analyse; Fast-Fourier-Transformation \texttt{fft} (Umwandlung in Spektrum), \texttt{getSubSample} (Herstellen einer Überlappung mit den zeitlichen Nachbarn), \texttt{getSubReady} (Zeropadding, s. \ref*{loesung})

\paragraph{Convthat.py:} Zuerst als Datei für für die Quasi-Faltung gedacht \texttt{convthat}. Beinhaltet auch die lokale Maximafindung \texttt{locmax} und die Lösung für das Superpositionieren \texttt{findTimbre}.

Importiert Timbrefinder.py

\paragraph{Timbrefinder.py:} Definiert den Algorithmus um das Least-Absolute-Problem zu lösen.

\paragraph{Notefinder.py:} Ist noch nicht fertig und eingebunden. Sorgt für die Diskretisierung der Pitch- und Amplitudenverläufe in Noten.

\paragraph{Trainer.py:} Arbeitet Samples in Unterordnern ab und Verarbeitet diese Zu Obertonreihendatensätzen.

Der in Abschnitt \ref{loesung} abgezeichnete Algorithmus, lässt viele frei wählbare Parameter offen. Dabei werden die wichtigsten hier aufgelistet.

• p - Anzahl der untersuchten potentiellen Grundtönen

• Die Anzahl der gegebenen Beispiel-Obertonverteilungen

• Kern für die Quasi-Faltung um $Y_c$ zu bestimmen

• Kern für die Glättung vom Spektrogramm in Zeitachse, in Frequenzachse, Tonstärke, und Tonfrequenz

Das variieren dieser Parameter kann die Genauigkeit erhöhen. Allerdings gibt es keine allgemeine optimale Lösung und ist vom Anwendungsfall abhängig. \paragraph{Beispiel}Wird $p$ erhöht, so ist zwar die Chance geringer dass ein Grundton übersehen wird, aber es gibt auch eine wesentlich höhere Chance dass Overfitting entsteht (siehe \ref{overfit}).

Für die Obertonverteilungen wurde ein kleines Trainerprogramm geschrieben, welches aus mehreren Samples eine Charakteristische Verteilung für Anschlag, Haltung und Ausklingzeit, für verschiedene Grundtöne und für verschiedene Instrumente. Dies führt zur Zeit nur in bestimmten Fällen zu einer Verbesserung.

\label{overfit} In der Least-Absolute-Regression wird ein \textquotedblleft überbestimmtes\textquotedblright\ System $A\cdot x\approx b$ gelöst. Dabei ist der $\mathrm{Rang}(A)\le\mathrm{Dim}(b)$. Im Fall das der Rang von $A$ gleich der Dimension von $b$ ist, gibt es ein $x$ für das $A\cdot x=b$ gilt. Dies kann auch bei willkürlichen Obertonverteilungen der Fall sein. Nun kann es analog bei $\mathrm{Rang}(A)<\mathrm{Dim}(b)$ zu einem zu guten Ergebnis führen, wenn der Rang nicht klein genug ist, da durch eine zu gute Superposition der Spalten in $A$ ein gutes Ergebnis erfasst wird, welches allerdings nicht das gesuchte Ergebnis wiederspielt. Dies ist zwar kein mathematischer Beweis aber soll eine kleine Veranschaulichung sein. Man könnte es auch romantisch erklären indem sich der genialste Musiker des Landes vorgestellt wird, welcher ein ganzes Orchester so spielen lässt, sodass kein einziger Ton zu hören ist. Da sich alle Instrumente gegenseitig auslöschen, kann nun der zweitbeste Musiker des Landes nicht mehr nachvollziehen, welche Noten gespielt werden.

Als Lösung, für Obertöne, welche sich gegenseitig auslöschen, soll nicht nur der Absolutbetrag der Fourier-Transformation sondert auch die Phase miteinbezogen werden. Somit soll es dem Algorithmus ermöglicht werden, sich auslöschende Obertöne zu erkennen. Der Gedanke ist keine Information zu verwerfen.

Die Laufzeit des Algorithmus ist von $\mathcal{O}(\tilde{m})$, da die die Sections immer die gleiche Länge haben und der Algorithmus jede Section einzeln auswertet. Eine Faltung mit konstanten Kern ist auch von $\mathcal{O}(\tilde{m})$. Es gibt nun drei offensichtliche Möglichkeiten den Algorithmus zu optimieren.

• Multithreading

Da der Algorithmus nicht viel Arbeitsspeicher verbraucht, und sehr viele Sections einzeln unabhängig voneinander berechnet, ist er sehr parallelisierbar. Dies ist ideal für mehrkernige Prozessoren wie Grafikkarten oder Multicore-CPUs. Solange es mehr Kerne als Sections gibt hat der Algorithmus somit sogar eine Ordnung von $\mathcal{O}(1)$.

• Portierung zu einer schnelleren Programmiersprache

Da um viele schleifen nicht drum herum gekommen wird sollte Cython oder eine richtige C-Implementierung benutzt werden.

• Code-Optimierung

Der Code kann an vielen Stellen noch verbessert werden um bessere Leistung zu erzielen, da es vorerst um die Genauigkeit des Algorithmus ging.

Das Projekt ist noch nnicht fertig, aber jetzt schon ein erfolg. Die Polyphone Notenfindung ist ein relativ schweres Problem und funktioniert schon im Ansatz. Das Projekt selber hat ein breites Spektrum an mathematischen Wissen und musikalischen Grundlagen abgefragt. Wie in den meisten Projekten ist der Arbeitsaufwand im Vorhinein schwer abschätzbar und somit ist auch dieses Projekt durch die schlechte Planung nicht rechtzeitig fertig geworden.