Projektlabor Robotik MINTgrün

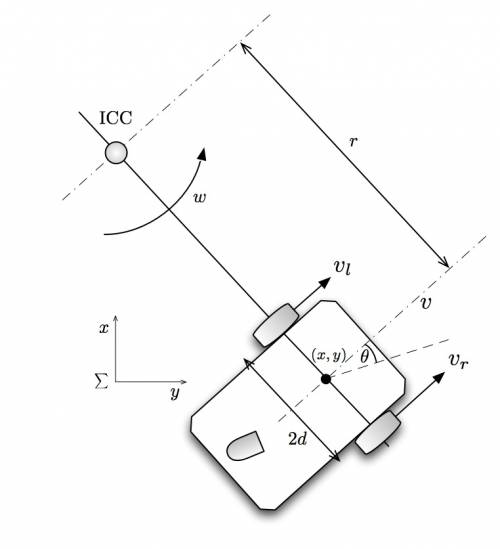
Ein Roboter mit Differenzialantrieb verfügt über zwei Räder die auf einer Achse im Abstand $2d$ angeordnet sind. Die Räder werden unabhängig voneinander angetrieben. Ein eventuell nötiges Stützrad wird nicht angetrieben. Wir bezeichnen die Geschwindigkeit des rechten bzw. linken Rades mit $v_r$ und $v_l$, und die Gesamtgeschwindigkeit mit $v$. Solange die Geschwindigkeiten der Räder konstant sind und $v_l \neq v_r$ gilt, beschreibt der Roboter eine Kreisbahn mit konstanter Rotationsgeschwindigkeit $w$. Das Zentrum der Drehung wird ICC (Instantaneous Center of Curvature) genannt. Diesen Umkreist der Roboter mit Radius $r$ (siehe Abb. 1).
Die nachfolgenden Überlegungen sind im wesentlichen eine Zusammenfassung aus den Skripten http://www.uni-ulm.de/fileadmin/website_uni_ulm/iui.inst.130/Mitarbeiter/oubbati/RobotikWS1113/Folien/Differentialantrieb.pdf und http://www.ki.informatik.hu-berlin.de/lehre/ws0506/kogrob/KR0506Bewegung-kurz.pdf, sowie des Tutorials http://rossum.sourceforge.net/papers/DiffSteer/DiffSteer.html.

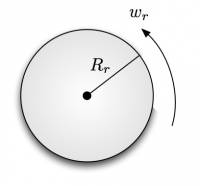
Zunächst betrachten wir das rechte Rad des Roboters (siehe Abb. 2). Aus dem Radius $R_r$ und der Rotationsgeschwindigkeit $w_r$ können wir direkt die Geschwindigkeit $v_r$ bestimmen. Eine weiter Möglichkeit $v_r$ zu bestimmen, ergibt sich aus Abb. 1. Jeder sollte sich den folgenden Zusammenhang klar machen: \begin{align*} R_r \cdot w_r = v_r = (r + d) \cdot w \end{align*}

Die Geschwindigkeit des Roboters lässt sich nun folgendermaßen beschreiben: \begin{align} v &= \frac{v_l + v_r}{2}\\ w &= \frac{v_r - v_l}{2d} \end{align} Die Distanz zum ICC wird dann: \begin{align} r &= d\frac{v_l + v_r}{v_r - v_l} \end{align} Welche Bewegungszustände ergeben sich für $v_l = v_r$ und $v_l = -v_r$?

Wir wollen nun die Position des Roboters im Weltkoordinatensystems $\sum$ bestimmen. Im 2-dimensionalen reichen uns zur bestimmung der Position und Orientierung drei Werte $< x,y,\theta >$. Wir gehen dabei von einer Anfangsposition des Roboters zum Zeitpunkt $t = 0$ aus, $P(t = 0) = (0,0,0)$. Bewegt sich der Roboter nun im Zeitintervall $\delta t = [0,t]$, mit einer Geschwindigkeit $v$ und einer Winkelgeschwindigkeit $w$, erhalten wir die neue Position $P(t) = (x(t),y(t),\theta(t))$.
Für die Geschwindigkeit in $x$- bzw. $y$-Richtung zum Zeitpunkt $t$, nutzen wir folgenden einfachen Zusammenhang aus: \begin{align*} v_x(t) &= v(t) \cos{(\theta)} \\ v_y(t) &= v(t) \sin{(\theta)} \end{align*} Wollen wir nun die neue Position des Roboters bestimmen, brauchen wir lediglich über das Zeitintervall $[0,t]$ zu integrieren. Dazu nehmen wir an das $v(t)$ in $\delta t$ konstant ist und $v_r \neq v_l$ gilt: \begin{align} \theta(t) = \int_0^t w(\tau)d\tau &\overset{(2)}{=} \int_0^t \frac{v_r - v_l}{2d}d\tau = \frac{v_r - v_l}{2d} t \end{align} Nun können wir die $x$-, $y$-Position mit Hilfe von (4) bestimmen: \begin{align} x(t) &= \int_0^t v_x(\tau)d\tau = \int_0^t v(\tau)\cos{(\theta(\tau))}d\tau \notag\\[1.0em] &\overset{(1)}{=} \frac{v_l + v_r}{2} \int_0^t \cos{\biggl(\frac{v_r - v_l}{2d}\tau\biggr)}d\tau \notag\\[1.0em] &= d\frac{v_l + v_r}{v_r - v_l} \sin{\biggl(t\frac{v_r - v_l}{2d}\biggr)} \end{align} Und \begin{align} y(t) &= \int_0^t v_y(\tau)d\tau = \int_0^t v(\tau)\sin{(\theta(\tau))}d\tau \notag\\[1.0em] &\overset{(1)}{=} \frac{v_l + v_r}{2} \int_0^t \sin{\biggl(\frac{v_r - v_l}{2d}\tau\biggr)}d\tau \notag\\[1.0em] &= d\frac{v_l + v_r}{v_r - v_l} \biggl(1-\cos{\biggl(t\frac{v_r - v_l}{2d}\biggr)\biggr)} \end{align} Für den Spezialfall das $v_r = v_l$ ist, erhalten wir folgenden Zusammenhang: \begin{align*} x(t) &= \frac{v + v}{2} \int_0^t \cos{\biggl(\frac{v - v}{2d}\tau\biggr)}d\tau = v \cdot t \\ y(t) &= 0 \\ \theta(t) &= 0 \end{align*} Zusammengefasst können wir die Bewegung des Roboters beschreiben als: \begin{align} x(t) &= \begin{cases} x_0 + d\frac{v_l + v_r}{v_r - v_l} \sin{\biggl(t\frac{v_r - v_l}{2d}\biggr)}& für & v_r \neq v_l \\ x_0 + vt \cos{(\Theta)}& für & v_r = v_l & und & \theta(0) = \Theta \end{cases}\\[1.0em] y(t) &= \begin{cases} y_0 + d\frac{v_l + v_r}{v_r - v_l} \biggl(1-\cos{\biggl(t\frac{v_r - v_l}{2d}\biggr)\biggr)} & für & v_r \neq v_l \\ y_0 + vt \sin{(\Theta)}& für & v_r = v_l & und & \theta(0) = \Theta \end{cases}\\[1.0em] \theta(t) &= \Theta + \frac{v_r - v_l}{2d} t \end{align} Die Startwerte $< x_0,y_0,\Theta >$ sind im einfachsten Fall gegeben durch $P(0) =\ < 0,0,0 >$

Es sollte immer beachtet werden das diese Formeln nur eine Näherung der realen Umstände darstellen. So wird z.B. die Beschleunigung des Roboters außer Acht gelassen, Reibungsverluste spielen eine Rolle und Ungenauigkeiten in der Messung der Radumdrehungen. G.W. Lucas empfiehlt, abhängig vom aufbau des Roboters, eine Winkeländerung von höchstens $10^{\circ}$. Jede größere Änderung sollte in mehrere Segmente unterteilt werden.
Einen tieferen Einblick gibt die oben aufgeführte Literatur.