Projektlabor Robotik MINTgrün

Mit dem Catmull-Rom-Algorithmus lassen sich aus vier bekannten Punkten $p_0$, $p_1$, $p_2$ und $p_3$, der Weg zwischen $p_1$ und $p_2$ interpolieren. Die nachfolgende Abbildung zeigt den berechneten Weg im Fall der uniform-Variante des Algorithmus.

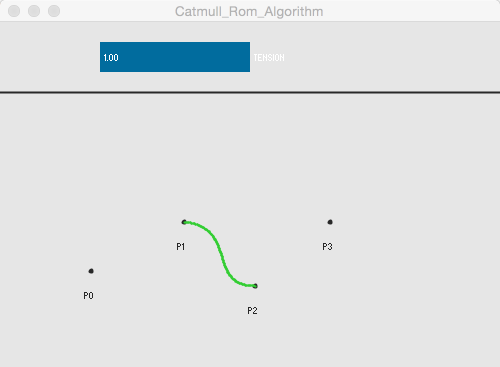
Der Vorteil dieses Verfahrens ist dass die berechnete Kurve immer durch die bekannten Punkte verläuft. Es besteht jedoch die Möglichkeit dass sich die Kurve innerhalb eines Abschnitts selber schneidet. Diesem Problem kann man begegnen indem man einen Faktor zum Glätten der Kurve verwendet. Dieser wird häufig als „tension“ bezeichnet. Nachfolgend verschiedene Werte des Glätt-Faktors.

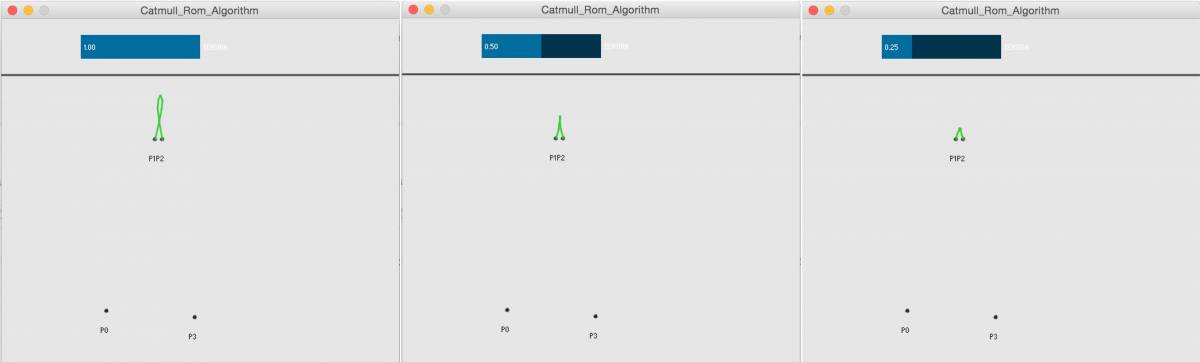
Da dieser Algorithmus vier Stützpunkte benötigt, ist es zunächst nicht möglich den Weg zwischen $p_0$ und $p_1$ bzw. $p_2$ und $p_3$ zu bestimmen. Ein einfacher hack für dieses Problem ist die Wahl der Punkte auf $\{p_0, p_0, p_1, p_2\}$ zu ändern.

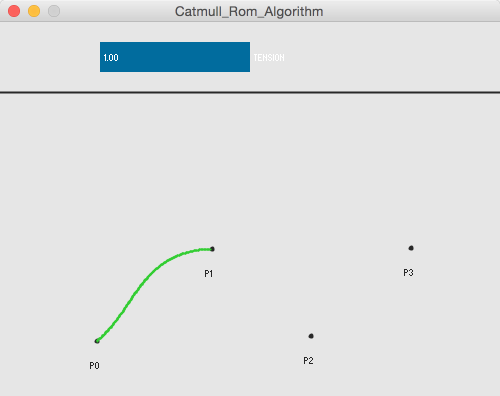
Eine umfassende Herleitung des Algorithmus findet ihr hier. Dieses Paper von Yuksel et. al. beschäftigt sich mit der Parametrisierung von Catmull-Rom-Kurven, wie etwa die Centripetal-Parametrisierung, welche garantiert dass sich die Kurve innerhalb eines Abschnittes nicht selbst schneidet.

Aus der oben genannten Herleitung erhalten wir die Basisfunktionen (In der numerischen analysis auch „blending functions“ genannt) der Kurve:

\begin{equation*} Mu = \begin{bmatrix} −\tau u+2\tau u^2 −\tau u^3 \\ 1+(\tau−3)u^2+(2−\tau)u^3 \\ \tau u+(3−2\tau)u^2 +(\tau −2)u^3 \\ −\tau u^2 +\tau u^3 \end{bmatrix} \end{equation*}

Dabei bezeichnet $\tau$ die „tension“ (Glätt-Faktor) welche Werte im Intervall $[0,1]$ annimmt und $u$ den Zeitpunkt an dem die Funktionen ausgewertet werden. Zu welchen Zeitpunkten die Funktionen ausgewertet werden hängt von der Parametrisierung ab, zum Beispiel wird bei der uniform-Parametrisierung eine feste Anzahl von Punkten gewählt. Die interpolierte Koordinate ergibt sich nun aus dem Produkt der Matrix eurer Stützpunkte und dem Vektor eurer Basisfunktionen.

\begin{equation*} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x_{p_0} & x_{p_1} & x_{p_2} & x_{p_3} \\ y_{p_0} & y_{p_1} & y_{p_2} & y_{p_3} \end{bmatrix} \cdot \begin{bmatrix} −\tau u+2\tau u^2 −\tau u^3 \\ 1+(\tau−3)u^2+(2−\tau)u^3 \\ \tau u+(3−2\tau)u^2 +(\tau −2)u^3 \\ −\tau u^2 +\tau u^3 \end{bmatrix} \end{equation*}