Benutzer-Werkzeuge
Seitenleiste
Inhaltsverzeichnis
Wir haben nichts auszusetzen. ![]()
Verkehrssimulation
von Seohyun Bae und Jonathan Pittrof
Was kann unsere Simulation?
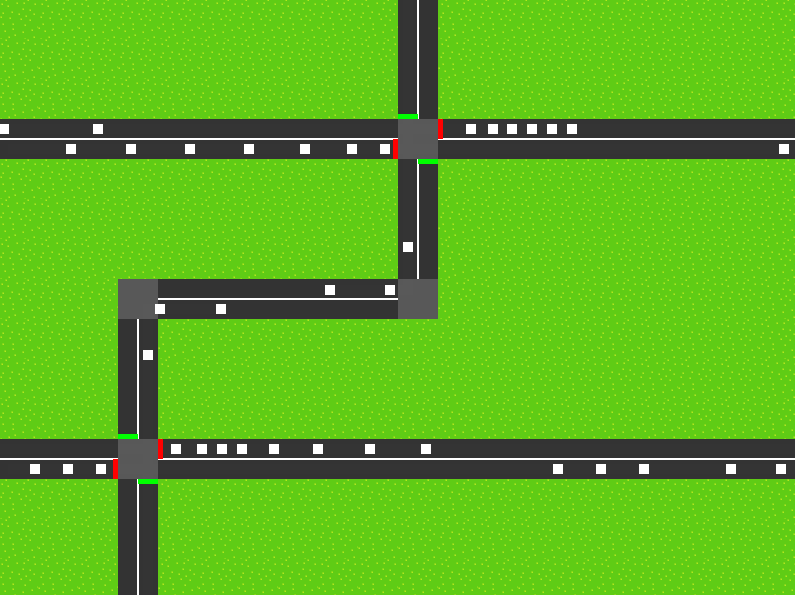
Mit der von uns entwickelten Verkehrssimulation kann ein einfaches Straßennetz mit Kurven, Kreuzungen und einspurigen Fahrbahnen angelegt werden und anschließend der Verkehrsfluss mit beliebig vielen Fahrzeugen betrachtet werden. Den Fahrzeugen können dabei Eigenschaften, wie Wunschgeschwindigkeit, Maximalbeschleunigung und Reaktionszeit übergeben werden. An den Kreuzungen gibt es die Möglichkeit, Ampelschaltungen anzupassen und die daraus resultierenden Veränderungen zu betrachten.
Projektplanung
Ursprüngliches Ziel:
Unser ursprüngliches Ziel war es, einen kleinen Ausschnitt von Berlins Straßennetz in unser Programm zu übernehmen und anschließend zu optimieren.
Zwischenziele
- OpenGL, pygame und pyglet Grundlagen verstehen
- Ein Fahrzeug, dass beschleunigen, bremsen und Kurven fahren kann
- Kleines Teststraßennetz
- Ampeln, Spuren, Geschwindigkeitsbeschränkungen, Vorfahrtsregeln
- Fahrzeuge können Hindernisse wahrnehmen
- Kollisionen bzw. gegenseitige Wahrnehmung der Fahrzeuge
- Benutzeroberfläche
Verwendete Literatur
- TREIBER, Martin und Arne KERSTING, 2010. Verkehrsdynamik und -simulation: Daten, Modelle und Anwendungen der Verkehrsflussdynamik. Heidelberg: Springer. ISBN 978-3-642-05227-9
- HARMS, Volker, 2004. Physik für Mediziner und Pharmazeuten. Unbekannter Ort: Harms-Verlag. ISBN 978-3860261118
Andere Hilfsmittel:
- Pygame Tilemap Tutorial: http://usingpython.com/pygame-tilemaps/
- PyOpenGL Tutorial 2: http://www.labri.fr/perso/nrougier/python-opengl/
- PyOpenGL Tutorial 3: https://isis.tu-berlin.de/mod/url/view.php?id=640594
- pyglet Dokumentation: https://pyglet.readthedocs.io/en/pyglet-1.3-maintenance/
- Simulationsbeispiele: http://traffic-simulation.de/
Aufgabenverteilung
Jonathan:
- Grafische Umsetzung (also anfangs noch PyOpenGL, später dann PyGame)
- Programmgrundstruktur aus drei Klassen und einem
Loop, der ständig ausgeführt wird - Die Methoden
change,fahre,zeichne,pruefe_ampel,pruefe_kollision,zeichne_fahrbahn,zeichne_ampel,phasen - Das „eckige“, aber zuverlässige Abbiegen der Fahrzeuge
- Die Wiki
Seohyun:
- Das „runde“ Abbiegen der Fahrzeuge
- Die Methoden
fahreundpruefe_ampelfür das Abbiegen angepasst - Die
init-Methoden angefangen - Die Erklärung zur
abbiegen-Methode in der Wiki
Protokolle
Unsere wöchentlichen Protokolle gibt es hier: ws1819:verkehrssimulation:Protokolle
Dokumentation
Unser Programm besteht aus den drei Klassen Fahrzeug, Fahrbahn und Ampel. Bei der visuellen Darstellung haben wir uns letztendlich für PyGame entschieden, da dieses viel einfacher ist, als PyOpenGL und für unsere Simulation vollkommen ausreicht.
Das Programm besitzt eine Haupt-Schleife, die mehrfach in der Sekunde ausgeführt wird. In jedem Zeitschritt des Programms wird zuerst der Hintergrund, also das Straßennetz mit Pygame gezeichnet:
for row in range(maphoehe): for column in range(mapbreite): screen.blit(textures[tilemap[row][column]],(column*kachelgroesse,row*kachelgroesse))
Danach werden alle Ampeln an ihre angegebenen Positionen gezeichnet und zum Schluss die Fahrzeuge, für die nacheinander alle Methoden der Klasse Fahrzeug ausgeführt werden.
Die Klasse ''Fahrzeug''
Jedes Objekt der Klasse Fahrzeug hat 13 Attribute:
- x- und y-Koordinaten
- Fahrtrichtung
- Geschwindigkeit
v - Beschleunigung
a - Wunschgeschwindigkeit und Tempolimit
v_optimalundv_original - Maximalbeschleunigung und Maximalbremsbeschleunigung
a_maxunda_negativ_max - Reaktionszeit
- Länge
l - Farbe
- Die Fahrbahn, auf der sich das Fahrzeug gerade befindet
Die ''change''-Methode
Diese Methode vergleicht die Wunschgeschwindigkeit v_optimal mit der aktuellen Geschwindigkeit v jeden Fahrzeuges und entscheidet dementsprechend, ob das Fahrzeug beschleunigen oder bremsen soll. Die entsprechend berechnete Beschleunigung wird dann als Wert für a festgelegt.
Die ''fahre''-Methode
fahre ist dafür zuständig, aus der aktuellen Geschwindigkeit und Beschleunigung, die neuen Koordinaten von jedem Fahrzeug zu berechnen. Dazu wird zuerst die Fahrtrichtung geprüft und dann mit der Formel
\[\frac{1}{2} \cdot a \cdot t^2 + v0 \text{ (Anfangsgeschwindigkeit) } \cdot t + s0 \text{ (bereits zurückgelegter Weg) }\]
die neuen Koordinaten berechnet. Außerdem wird die Geschwindigkeit mit
\[v = a \cdot t + v0\]
aktualisiert.
Die ''zeichne''-Methode
Diese Methode prüft, ob sich das Fahrzeug aus dem Fenster bewegt und setzt es dann wieder an den Anfang der Straße. Außerdem wird das Fahrzeug mit der Methode
pygame.draw.rect(screen, Farbe, [x, y, Breite, Höhe], 0)
an die entsprechende Stelle in das PyGame-Fenster gezeichnet. Die Null am Ende des Befehls bedeutet, dass das gezeichnete Rechteck mit Farbe ausgefüllt wird.
Die ''abbiegen''- Methode
Mit dieser Methode hatten wir einige Schwierigkeiten. Letztendlich hatten wir zwei verschiedene Programme, eines wo die Fahrzeuge zwar in einem schönen Bogen abbiegen, dafür aber häufig nach dem Abbiegevorgang nicht mehr ganz gerade weiterfahren und in den Gegenverkehr geraten. In dem zweiten Programm biegen die Fahrzeuge, ohne einen Bogen zu fahren einfach abrupt um 90° ab, bleiben dafür aber zuverlässig auf ihrer Fahrbahn.
Das runde abbiegen funktioniert so:
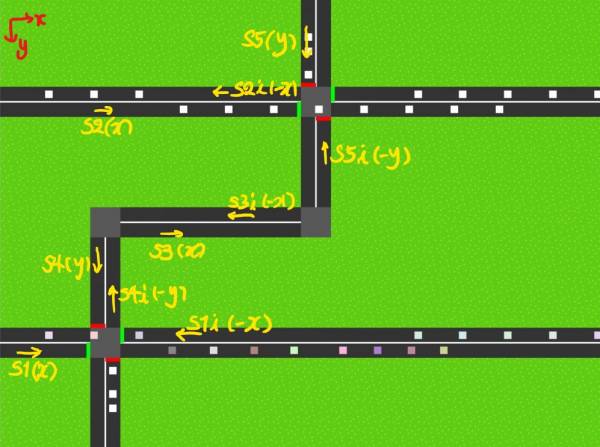
Jede Fahrbahn hat ihre eigene Richtung(Vektor) und eine Fahrzeugliste, mit allen Fahrzeugen die auf dieser Straße fahren. Jedes Fahrzeug gehört der Straße, auf der das Fahrzeug ist, und fährt in die Richtung von der Straße. Es gibt vier Richtungen, und zwar: x, -x, y und -y.
Wenn ein Fahrzeug nur in einer diesen Richtungen fahren kann, biegt es eckig ab.
Wie kann ein Fahrzeug denn so eine Kurve fahren?
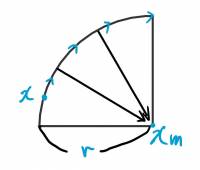
Eine kreisförmige Bewegung ist mit einer ständigen Änderung der Bewegungsrichtung verbunden. Zur Änderung der Bewegungsrichtung ist eine beschleunigende Kraft notwendig.
Die Kraft, welche den Körper in einer Kreisbahn hält, ist auf das Zentrum gerichtet und heißt Zentripetalkraft.
\[|\vec{a}(t)| = \frac{|\vec{v}(t)|^2}{r}\] Das ist die Skala von der Zentripetalbeschleunigung. \(r\) ist der Radius des Kreises.
Und aufgrund des Geschwindigkeit-Zeit-Gesetzes kann die Geschwindigkeit als Vektor so beschrieben werden:
\[\vec{v}(t + \Delta{t}) = \vec{v}(t) + \vec{a}(t)\Delta{t}\] Da die Beschleunigung hier Zentripetalbeschleunigung ist, kann \(\vec{a}\) so ersetzt werden:
\[\vec{v}(t + \Delta{t}) = \vec{v}(t) + \left[\frac{|\vec{v}(t)|^2}{r}\right] \left[\frac{(\vec{x_m}-\vec{x}(t))}{|\vec{x_m}-\vec{x}(t)|}\right]\Delta{t}\]
\(\vec{x_m}\) ist der Mittelpunkt des Kreises und \(\vec{x}(t)\) ist der aktuelle Ort zum Zeitpunkt \(t\).
\(\left[\frac{|\vec{v}(t)|^2}{r}\right]\): Das ist die Skala der Beschleunigung.
\(\left[\frac{(\vec{x_m}-\vec{x}(t))}{|\vec{x_m}-\vec{x}(t)|}\right]\): Das ist die Richtung/der Vektor, die/der immer auf das Zentrum gerichtet ist.
Da \(r = |\vec{x_m}-\vec{x}(t)|\) ist, kann die Formel nochmal umgeschrieben werden:
\[\vec{v}(t + \Delta{t}) = \vec{v}(t) + \frac{|\vec{v}(t)|^2}{|\vec{x_m}-\vec{x}(t)|^2} (\vec{x_m}-\vec{x}(t)) \Delta{t}\]
Damit können wir während des Abbiegens die Vektor-Geschwindigkeit nach \(dt\) aktualisieren. Jeder Vektor hat zwei Elemente: x-Koordinate(x) und y-Koordinate(y). Deswegen können wir damit jeweils x-Geschwindigkeit und y-Geschwindigkeit berechnen und jeweils x-Koordinate(x) und y-Koordinate(y) auch.
Nach dem Abbiegen ist das Fahrzeug nicht mehr auf der vorigen Straße, sondern auf der neuen Straße. Deswegen entfernen wir das Fahrzeug aus der Fahrzeugliste von der vorigen Straße, und fügen das zur Fahrzeugliste von der neuen Straße. Das Fahrzeug hat neue Richtung, die der Straße gehört, und fährt weiter.
Die ''prüfe_ampel''-Methode
Auch bei dieser Methode wird zuerst geprüft, in welcher Richtung das Fahrzeug unterwegs ist. Danach wird zu jeder Ampel, die das Fahrzeug passieren könnte der Abstand ausgerechnet. Sobald die Ampel rot oder gelb ist und der Abstand zur Ampel gering genug ist, wird die Wunschgeschwindigkeit des Fahrzeuges auf Null gesetzt, sodass es beim nächsten Durchlauf der change-Methode beginnt zu bremsen.
Der Programmcode für die Fahrtrichtung x sieht so aus:
if self.richtung == "x": for i in self.strasse.ampelliste: dist = i.x - self.x disty = i.y - self.y if disty < 20 and disty > -20: if dist < 55 and dist > 0 and i.zustand == 2: self.v_optimal = 0 elif dist < 55 and dist > 0 and i.zustand == 1: self.v_optimal = 0
Die ''prüfe_kollision''-Methode
Der Name dieser Methode ist etwas missverständlich, denn eigentlich dient diese Methode dazu, Kollisionen durch rechtzeitiges Abbremsen zu verhindern. Dazu gibt es eine global zugängliche Liste belegt[]. Diese Liste enthält immer alle aktuellen x- und y-Koordinaten von jedem Fahrzeug. Nacheinander wird jedes Element dieser Liste betrachtet und der x- und y-Abstand zum aktuellen Fahrzeug, unter Beachtung der Fahrzeuglänge, ausgerechnet. Wenn sich das jeweils betrachtete Fahrzeug weniger als 5 Pixel links oder rechts vom aktuellen Fahrzeug befindet, wird als nächstes geschaut, wie weit das Fahrzeug aus der Liste sich vor, oder hinter dem aktuellen Fahrzeug befindet. In dynamischen Intervallen (doppelter Sicherheitsabstand, Sicherheitsabstand, halber Sicherheitsabstand und zu nah), wird die Geschwindigkeit des aktuellen Fahrzeugs entsprechend angepasst. Als Sicherheitsabstand nehmen wir die Faustformel Halber Tacho = Sicherheitsabstand. Sollte festgestellt werden, dass sich kein Fahrzeug im relevanten Bereich vor dem aktuellen Fahrzeug befindet, wird die Wunschgeschwindigkeit auf die Maximal erlaubte Geschwindigkeit gestellt. Das bewirkt auch, dass das Fahrzeug an einer grün gewordenen Ampel wieder losfährt (die Wunschgeschwindigkeit wird an einer roten Ampel auf 0 gesetzt).
for i in range(0, len(belegt)): if self.richtung == "x": distx = belegt[i][0] - (self.x + self.l) disty = belegt[i][1] - (self.y) if disty < 5 and disty > -5: if distx < 10 and distx > 0: self.v = 0 elif distx < self.v and distx >= self.v/2: self.v = -1 * dt * 100 + self.v elif distx < self.v/2 and distx >= self.v/4: self.v = -3 * dt * 100 + self.v elif distx < self.v/4 and distx >= 0: self.v = self.a_negativ_max * dt * 100 + self.v else: self.v_optimal = self.v_original elif self.richtung == "y": . . .
Die Klasse ''Fahrbahn''
Die Klasse Fahrbahn hat die Attribute Startkachel, Endkachel, Fahrtrichtung, Fahrzeugliste und Ampelliste.
Die ''zeichne_fahrbahn''-Methode
Diese Methode dient dazu, die Fahrbahntexturen und Kreuzungstexturen an die entsprechenden Stellen der Tilemap einzufügen. Dazu werden die Koordinaten der Startkachel und Endkachel ausgelesen und zwischen diesen Kacheln die Straße gezeichnet.
Die Kacheln werden nach diesem Muster abgespeichert, also als Liste in einer Liste:
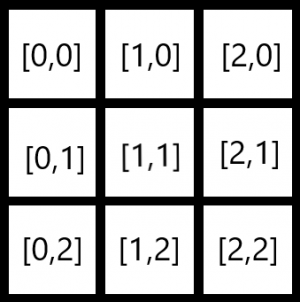
Der Programmcode für Fahrbahnen in x-Richtung sieht so aus:
if self.f_richtung == "x": for i in range(self.startkachel[0],self.endkachel[0]): tilemap[self.startkachel[1]][i] = 4
Die ''fuege_fahrzeug_hinzu''- und ''fuege_ampel_hinzu''-Methode
Diese beiden Methoden speichern einmalig alle Fahrzeuge und alle Ampeln in jeweils einer eigenen Liste für jede Fahrbahn ein. Diese Listen werden dann später ständig mit den aktuellen Daten aktualisiert.
Die Klasse ''Ampel''
Die Klasse Ampel hat folgende Attribute:
- x- und y-Koordinaten
- Ausrichtung
- Zustand (0 für grün, 1 für gelb, 2 für rot)
- rot_dauer
- gruen_dauer
- timer
- q (zum abspeichern der vorherigen Ampelfarbe)
Die ''zeichne''-Methode
Diese Methode zeichnet, abhängig von der Ausrichtung der Ampel, ein Rechteck auf die entsprechende Stelle auf der Kreuzung.
pygame.draw.rect(screen, ampelfarben[self.zustand], [self.x, self.y, 5, 20], 0)
ampelfarben ist eine Liste mit RGB-Farbcodes für die verschiedenen Ampelfarben, also z.B. [255,0,0] für rot
Die ''phasen''-Methode
Diese Methode steuert die Ampelphasen. Bei jedem Aufruf wird der timer jeder Ampel um t (ist normalerweise 1) erhöht. Sobald der Timer einen bestimmten Wert überschritten hat, schaltet die Ampel um. Von rot und grün wird immer auf gelb geschaltet, von gelb, wird abhängig von q auf rot oder grün geschaltet.
Fazit
Mit unserem fertigen Programm haben wir leider nicht alles erreicht, was wir erreichen wollten. Was uns insbesondere noch fehlt, sind Vorfahrtsregeln, Unterschiedliche Fahrertypen, Abbiegen an Kreuzungen, mehrspurige Fahrbahnen, Kreisverkehre und maßstabsgetreue Geschwindigkeiten und Entfernungen. Vieles von dem wäre mit mehr Zeit noch gut umsetzbar gewesen. Wir haben uns vor allem geärgert, so viel Zeit in PyOpenGL gesteckt zu haben, um es am Ende dann doch durch Pygame zu ersetzen.
Trotzdem sind wir insgesamt ganz zufrieden mit der Simulation. Gut gefällt uns zum Beispiel die Performance: selbst mit 50 gleichzeitig simulierten Fahrzeugen, fällt die Framerate nicht unter 100fps. Und obwohl die Simulation im Detail nicht auf geprüften Daten beruht, lässt sich doch ein ganz guter Gesamteindruck von einer Verkehrssituation gewinnen, der sich wahrscheinlich nicht allzu sehr von der Realität unterscheidet.
Der Code
Es gibt zwei Versionen des Programms:
fertig_eckig.pyläuft stabil und zuverlässigfertig_rund.pydie Fahrzeuge fahren in den Kurven einen schöneren Bogen, es gibt aber noch Programmfehler