Benutzer-Werkzeuge
Seitenleiste
Eine sehr schöne Ausarbeitung einer sehr schönen Arbeit, ich hätte nur Kleinigkeit zu bemerken:
- In der Formel für die Beschleunigung verstehe ich $\hat{x}$ nicht, außerdem ist die Indizierung am Summenzeichen nicht ganz richtig. Ihr wollte über alle j mit $j\not = i$ summieren.
- Die Erklärung der höheren Genauigkeit des rk4-Verfahrens ist unklar. Was heißt 'viermal genauer'? Beim Euler-Verfahren erklärt ihr richtig, dass der Fehler bei einem Schritt quadratisch in der Schrittweite h (in der Zeit) ist. Bei rk4 ist der lokale Fehler durch $c h^5$ abzuschätzen.
- Vielleicht wäre es gut, bei der ersten Erwähnung (Euler-Verfahren) des Begriffs „Ordnung eines Verfahrens“ zu erklären, dass ein Verfahren von n. Ordnung heißt, wenn es einen lokalen Fehler $\sim h^5$ hat.
- Eigentlich habe ich mir vorgestellt, dass die Planungselemente im Hauptteil zu finden sind. Da aber eure Protokolle ausführlich und gut lesbar sind, ist es auch so in Ordnung.
Inhaltsverzeichnis
- Ziel
- Dokumentation
- Protokoll
- Analyse
- Fazit
- Ergebnis
- Credits
Mithilfe von Python möchten wir ein System von Himmelskörpern simulieren, das durch die gravitativen Kräfte und andere Einflüsse berechnet wird. Die Ergebnisse sollen graphisch dargestellt werden und interaktiv nutzbar sein.
Die ermittelten Daten sollen mit Berechnungen der NASA und ESA abgeglichen werden, um so die Korrektheit der Simulation abzuschätzen. Des Weiteren möchten wir verschiedene Simulationsalgorithmen verwenden, darunter die Euler-Methode, das Leapfrog-Verfahren und das Runge-Kutta-Verfahren 4.Ordnung, um diese zu vergleichen und entsprechend ihrer Korrektheit zu bewerten.
Je nach Fortschritt können wir im späteren Verlauf des Projekts Überlegungen zu weiterführenden Fragestellungen bzw. Visualisierungen angestellt werden. Hier sind z.B. die Berechnung von Gezeitenkräften, Kollisionsparameter oder Raumschiffen in Betracht zu ziehen.

Voraussetzungen:
Python 3.7
SkyField 1.10
Vpython 7.4
Numpy 1.15
Itertools
Programm
Programmcode
Verfahren
Unsere Simulation ist in der Lage das n-Körperproblem mittels drei unterschiedlicher Verfahren separat zu lösen und so für jeden Zeitschritt die neuen Positionen zu berechnen. Die Berechnungsverfahren unterscheiden sich zum Teil deutlich in den errechneten Werten, der Genauigkeit und der Stabilität.
Euler-Verfahren
Das explizite Euler-Verfahren ist das einfachste Verfahren zur Lösung numerischer n-Körperprobleme mittels Differentialgleichungen erster Ordnung.
Die Ordnung eines Verfahrens gibt an, wie genau das Verfahren in jedem Schritt arbeitet und wie stark der Fehler der Lösung durch Verringerung der Schrittweite abnimmt.
Um die neuen Positionen der Objekte im Raum zu ermitteln, werden zu erst die Gravitationskräfte, die zwischen alle Objekten wirken für jedes Objekt im Raum berechnet. Durch die berechnete Gravitationskraft ist es nun möglich die Beschleunigung für jedes Objekt mithilfe des 2. newton'schen Gesetzes (F=m*a), zu berechnen
Die Gleichung für die Berechnung der Beschleunigung von multiplen Körpern:
$$ a_{ix} = \sum_{j \neq i}^{i} \frac{Gm_j}{((x_i - x_j)^2 + (y_i - y_j)^2 + (z_i - z_j)^2)^\frac{3}{2}}(x_j - x_i) $$
Die Geschwindigkeit, Masse und Position der Objekte zum Simulationsbeginn ist bekannt, nun kann man mithilfe der berechneten Beschleunigung die neuen Positionen der Körper für einen festgelegten Zeitschritt berechnen.
Da sich die Beschleunigung kontinuierlich verändert, ist die Simulation umso genauer, desto kleiner die Zeitschritte festgelegt werden.
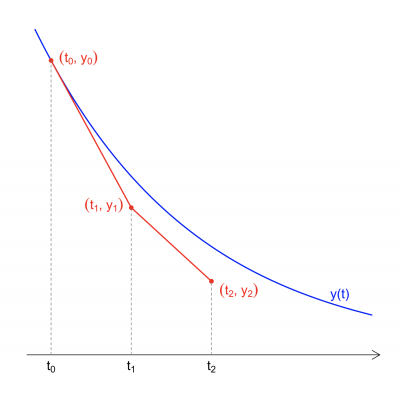
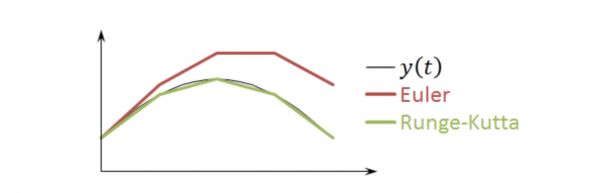
Bei einem linearen Verfahren der 1. Ordnung, ist der lokale Fehler(Fehler in einem Schritt) der Berechnung quadratisch zur Intervallgröße. In der Darstellung wird dies deutlich.
Leapfrog-Verfahren
Das Leapfrog-Verfahren ist ebenso wie das Euler-Verfahren eine Methode zur numerischen Integration von Differentialgleichungen. Die Leapfrog-Integration ist eine Methode der 2. Ordnung, jedoch benötigt es genauso viele Berechnungen pro Schritt wie das Euler-Verfahren. Dadurch ist das Leapfrog-Verfahren deutlich Genauer als das Euler-Verfahren und benötigt dabei keine zusätzlichen Berechnungsschritte. Beim Leapfrog-Verfahren ist die Berechnung der neuen Geschwindigkeit versetzt zur Berechnung der neuen Position.
- Berechnung der Kräfte
- Neue Geschwindigkeit basierend auf den Kräften und einem halben Zeitintervall berechnen
- Neue Position berechnen
- Neue Geschwindigkeit basierend auf einem halben Zeitschritt berechnen
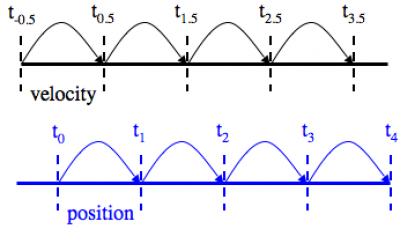
Es eignet sich daher sehr gut für gravitative Simulationen, da dort lediglich die Position der Objekte die Berechnung beeinflussen. Besonders die Eigenschaft der Reversibilität und der Symplektizität der Berechnung die Energie die in einem dynamischen System stabil bleibt, machen es zu einer konsistenten Methode zur Berechnung von Gravitationssystemen. Dies wird auch im Graphen des Leapfrog-Verfahrens deutlich.
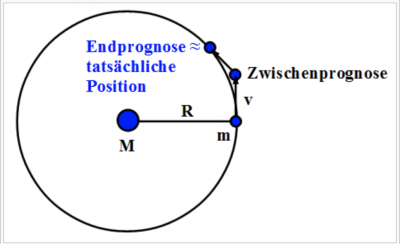
Runge-Kutta-Verfahren 4. Ordnung
Das Runge-Kutta-Verfahren (RK-Verfahren) basiert im Grunde auf dem Euler-Verfahren. Dies weist jedoch die Problematik auf, dass es von einer konstanten Beschleunigung innerhalb eines Zeitschrittes ausgeht, was jedoch nicht der Realität entspricht. Dies trifft im Grunde auch auf das Leapfrog-Verfahren zu, jedoch nur für einen halben Zeitschritt.
Das RK-Verfahren weist dieses Problem zwar immer noch auf, ist jedoch deutlich präziser als das Euler-Verfahren oder das Leapfrog-Verfahren. Es rechnet mit mehreren Beschleunigungswerten und bildet von diesen einen Durchschnittswert.
k1 = Beschleunigung basierend auf Startwerten
k2 = Beschleunigung 0.5 Zeitschritte (t = 0.5) vorwärts
k3 = Beschleunigung am Zeitschritt t = 0.5, mit der Beschleunigung von k2
k4 = Beschleunigung an t = 1 mit der Beschleunigung von k3
k1_v = self.calc_acceleration(n, positions, masses) k1_r = velocities k2_v = self.calc_acceleration(n, positions + k1_r * self.dt / 2, masses) k2_r = velocities + k1_v * self.dt / 2 k3_v = self.calc_acceleration(n, positions + k2_r * self.dt / 2, masses) k3_r = velocities + k2_v * self.dt / 2 k4_v = self.calc_acceleration(n, positions + k3_r * self.dt, masses) k4_r = velocities + k3_v * self.dt velocities = velocities + self.dt / 6 * (k1_v + 2*k2_v + 2*k3_v + k4_v) positions = positions + self.dt / 6 * (k1_r + 2*k2_r + 2*k3_r + k4_r)
Die Beschleunigungswerte werden gewichtet und ein Durchschnitt wird gebildet:
$$ Beschleunigung = \frac{ k_1 + 2 * k_2 + 2 * k_3 + k_4 }{6} $$
Mit diesem Verfahren wird ein lokaler Fehler von $$ \sim h^5 $$ und es wird dafür weniger Rechenleistung benötigt als z.B. mit dem Euler-Verfahren.

In unserem Protokoll haben wir unsere Fortschritte für jede Woche festgehalten, Probleme dokumentiert und Ziele bis zum nächsten Labor definiert. Zudem haben wir auch Aufnahmen vom WIP-Code und interessante Ergebnisse bzw. Probleme festgehalten.
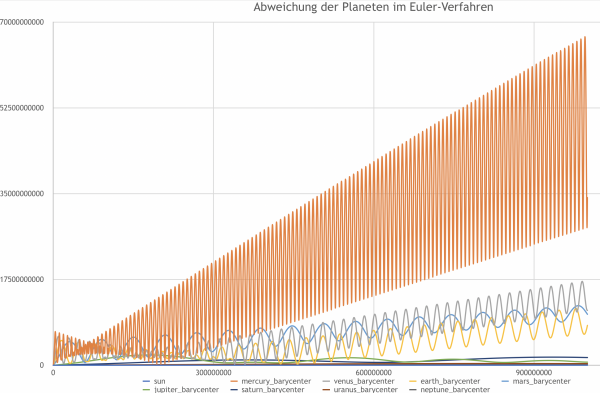
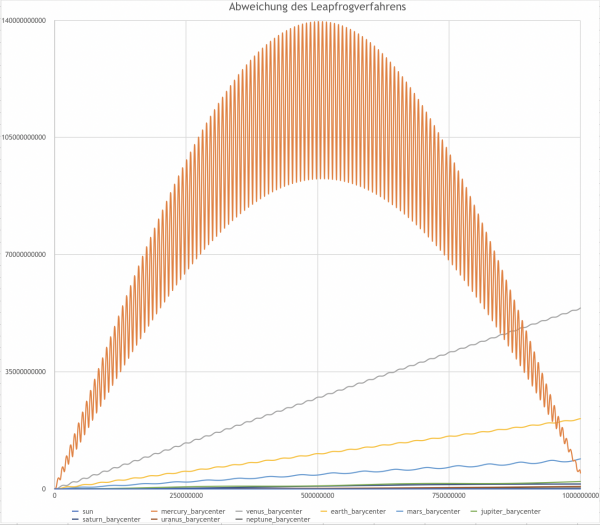
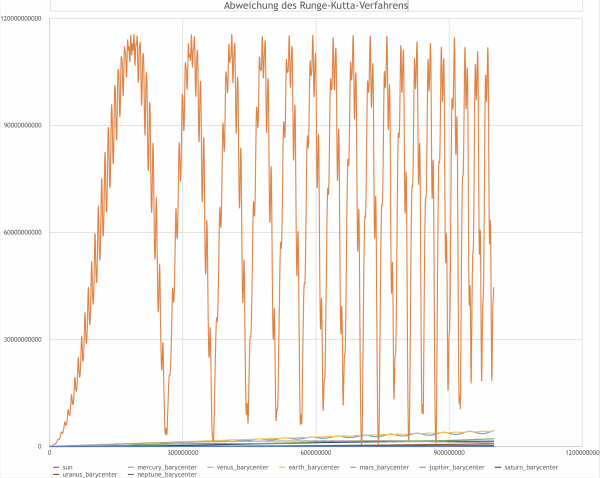
In den folgenden Graphen wird die absolute Entfernung der Planetenpositionen, die von uns berechnet wurden, zu den Positionen zum selben Zeitpunkt laut NASA deutlich, die mittels Skyfield in unserer Programm importiert wurden. Die Schrittlängen der Berechnungen wurden so gewählt, dass $ 10^9 $ Sekunden in der Simulation in ca. 50 Sekunden echter Zeit berechnet werden. So haben wir sozusagen die „Effizienz“ der Verfahren berechnet.
Auf den ersten Blick wird sofort deutlich, dass das Euler-Verfahren kein stabiles Berechnungsverfahren darstellt. Die Abweichung der Planeten, vor allem des Merkurs, geht offensichtlich gegen unendlich. Trotzdem bleibt sie in dem Zeitraum der Berechnung unter 70 Milliarden Metern. In dem Zeitraum der Berechnung ist das Euler-Verfahren also noch gar nicht so schlecht, verglichen mit den anderen Verfahren.
Bei Leapfrog und RK4 ist zu erkennen, dass die Abweichungen zwar gegen 140 bzw. 120 Millionen Meter geht, dabei aber symplektisch verläuft. Auf lange Zeit sind diese Verfahren also stabiler. Die großen Schwankungen lassen sich damit erklären, dass sich mit der Zeit eine Phasenverschiebung zwischen der Laufbahn der simulierten Planeten und den Solldaten entwickelt. Zu dem Zeitpunkt, an dem die Abweichung am größten ist, befindet sich der simulierte Planet also am gegenüberliegenden Punkt seiner Umlaufbahn wie der echte Planet. Die kleinen Schwankungen, die zum Zeitpunkt der größten Abweichung auch ihre maximale Amplitude erreichen, entstehen dadurch, dass die Umlaufbahnen der Planeten elliptisch sind. Wenn sich der Ist- und der Soll-Planet also an gegenüberliegenden Punkten der elliptischen Umlaufbahn befinden, schwankt ihre Entfernung am meisten, da der Durchmesser der Ellipse nicht konstant ist. Beim RK4-Verfahren lässt sich außerdem noch beobachten, dass die Planeten (zumindest der Merkur) mit der Zeit Energie verlieren und in eine nähere Umlaufbahn fallen. Dies kann man daran erkennen, dass die Schwankungen, die durch die Phasenverschiebung entstehen, immer kleiner werden, und dass der minimale Abstand nicht mehr die Null erreicht.

Zum Beginn des Labors, nach Findung unserer Projektidee, war unser Ziel eine n-Körpersimulation zu programmieren und diese graphisch darzustellen. Wir wollten des Weiteren das Programm so modular wie möglich gestalten, um so verschiedene Methoden und Visualisierungsmöglichkeiten zu erlauben und auch später noch zu erweitern. Diese Idee hat sich später bezahlt gemacht, da es uns nun möglich ist, die Simulation mit verschiedenen Berechnungen laufen und zu vergleichen lassen.
Es wurde auch schnell klar, dass wir zuerst das Sonnensystem als Anhaltspunkt für unsere Simulation nehmen, um so die Korrektheit der berechneten Werte zu überprüfen.
Letztendlich haben wir uns auf dieses System spezialisiert und unser Augenmerk auf den Vergleich der verschiedenen Berechnungsarten gelenkt. Nichtsdestotrotz ist es immer noch möglich, ein beliebiges System von Objekten zu erstellen und zu simulieren.
Es gab einige Schwierigkeiten in der Berechnung, da kleine Verständnisfehler das ganze System instabil werden haben lassen, doch nach einigen Stunden intensiver Fehlersuche und vielen Flüchen konnten wir die Berechnungen vollends abschließen.
Ein weiteres Problem stellte die Einarbeitung in Vpython dar, das wir jedoch letztendlich zufriedenstellend in Betrieb nehmen konnten.
Nächste Schritte in der Entwicklung wären Optimierungen der Berechnung für eine bessere Performance und andere Darstellungsmöglichkeiten zu implementieren.
Des Weiteren wäre es noch interessant, Möglichkeiten zu finden, um stabiles Systeme zu ermitteln und diese zu simulieren.
Wir sind mit dem Ergebnis des Projektlabores insgesamt sehr zufrieden und haben im Verlauf der Arbeit viel über Python, Differentialgleichungen und planetare Berechnungen gelernt. Es war insgesamt ein sehr interessantes Projekt, das wir in ähnlicher Form auch anderen Gruppen in Zukunft empfehlen würden, da man gut seine Erfolge sieht und eine angenehmes Maß an Programmierung und theoretischer Arbeit vor sich hat. Zudem muss man sich den Umgang mit diversen Werkzeugen beibringen, wie z.B. 3D-Rendering mit Vpython, der Umgang mit Datenspeicherung in Form von bspw. CSV-Files, mathematische Sachverhalte in Python implementieren, externe Programme wie Skyfield integrieren und vieles mehr.

Euler-Verfahren
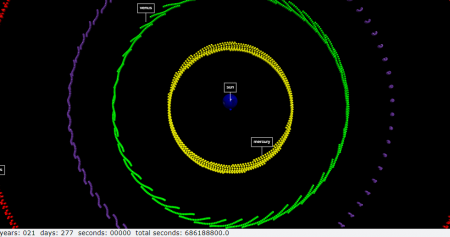
Leapfrog-Verfahren
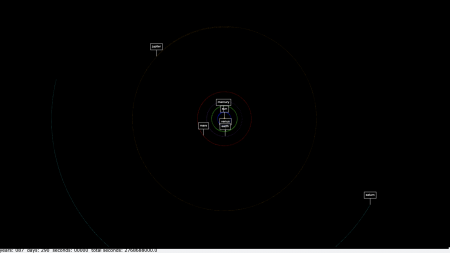
Lars Bonczek
Lukas Holdermann
Martina Kraußer
Lennox Lingk
Matthias Schuster