Benutzer-Werkzeuge
Seitenleiste
Inhaltsverzeichnis
Team:
Jakob, Ricardo, (ehem.) Maja
Thema:
Es wird folgendes Szenario zugrunde gelegt: n Züge mit unterschiedlichen Parametern (V_avg, Priorität,…) müssen in optimaler Reihenfolge auf ein Richtungsgleis zwischen Bahnhof A und Bahnhof B verteilt werden, sodass möglichst wenig Verspätung / Anschlussverluste entstehen, insbesondere wenn Züge mit Verspätung eintreffen.
Materialien:
Computer (optional)
Datensätze zu: Geschwindigkeiten/Durchschnittsgeschwindigkeiten verschiedener Zugkategorien, Prioritäten, Fahrgastzahlen, Taktdichten, Blockstellen, Zugfolgezeiten.
Grundlagen zur diskreten Optimierung
Dokumentation
Einleitung/Grundszenario
Wir befassen uns mit einem logistischen Problem, das seinen Ursprung in der Eisenbahn hat: Nach einer Streckensperrung sollen die im Bahnhof gestauten Züge in optimaler Reihenfolge ausgesandt werden. Es wird nur ein Richtungsgleis ohne Ausweichstellen betrachtet, das heißt es besteht keine Überholmöglichkeit.
In der Findungsphase stand auch noch die Idee eines Containerhafens im Raum. Bei diesem wäre das logistische Problem gewesen, die Container so zu stapeln, sodass möglichst wenige Containerbewegungen zum Umschlagen der Container in einer gewissen Zeitspanne vonnöten sind. Jedoch sprachen einige Dinge gegen diese Szenario:
- Die Grundstruktur mitsamt aller Rahmenbedingungen wäre deutlich schwerer und langwieriger Umzusetzen
- Keine so einfache Skalierbarkeit wie bei dem Eisenbahnproblem, wo schlichtweg mehr Züge aufgegleist werden.
Wie sieht eine optimale Reihenfolge aus?
Der einzige entscheidende Faktor ist die Verspätung der Reisenden bzw. Güter. Auf diese nehmen die geplante Ankunftszeit (wie straff ist der Fahrplan gestrickt), ggf. Umsteigezeiten und -zahlen (wie viele Personen möchten in welche Züge umsteigen), die Zuggeschwindigkeit, der minimale Zugfolgeabstand und die Länge der Strecke bis zur nächsten Ausweichmöglichkeit Einfluss.
All diese Eigenschaften sind im Programm frei wählbar.
Der Grundaufbau ist so konzipiert, dass einzelne Programmteile reibungslos ausgetauscht werden können:
BITTE DIE VERLINKTEN UNTERSEITEN IN DIESER AUFZÄHLUNG BEACHTEN
Beschreibung der Programmteile:
Implementierte Algorithmen:
Wichtig für die Algorithmen ist folgendes Modell zur Vorstellung: Alle Möglichen Lösungen (=ausgewertete Zugreihenfolgen) befinden sich auf einer Ebene. Nun wird je nach „Score“ der Auswertung diese Lösungen angehoben, es entsteht eine Hügellandschaft. Ziel eines jeden Algorithmus ist es nun, das „tiefste Tal“, also den geringsten Verspätungswert zu erreichen, und zwar in möglichst wenigen Schritten.
1. "Bruteforce"-Methode: Testen aller möglichen Kombinationen.
Der Algorithmus probiert alle Möglichen Kombinationen nacheinander aus und merkt sich immer die jeweils beste. Diese Methode garantiert eine optimale Lösung, da es aber n! Kombinationen bei n Zügen gibt, steigt die Laufzeit sehr schnell in nicht mehr sinnvolle Dimensionen (Auszug aus Protokoll:)
- 3 Züge: 0m00,073s
- 6 Züge: 0m12,757s
- 7 Züge: 2m04,064s
- 8 Züge: 20m55,436s
Der Code ist sehr simpel:
import itertools import simulation import auswertungsprogramm zug1={"vavg":20,"vist":20,"abfahrt":0,"besetzung":100,"ankunftplan":0,"ankunft":-1,"status":0,"nummer":595,"ort":2000} zug2={"vavg":30,"vist":30,"abfahrt":2,"besetzung":50,"ankunftplan":0,"ankunft":-1,"status":0,"nummer":123,"ort":0} zug3={"vavg":30,"vist":20,"abfahrt":4,"besetzung":20,"ankunftplan":0,"ankunft":-1,"status":0,"nummer":987,"ort":0} zuege = [zug1, zug2, zug3] def bruteforce(zugliste): #minimumzeit = auswertungsprogramm.auswertung(list(itertools.permutations(zugliste)[1])) for perm in itertools.permutations(zugliste): # Permutationen werden ermittelt temp = simulation.simuliere(list(perm)) # Permutationen werden gefahren bruteforce(zuege)
2. 2er-Tauschheuristik: Tauschen zufälliger Paare
Dieser Algorithmus wählt zufällig zwei Züge aus der Liste, vertauscht beide und testet die neu gewonnene Reihenfolge auf eine Verringerung der Verspätung. Die Laufzeit hängt lediglich davon ab, wie oft man das Programm tauschen lässt. Die Tauschzahl wird beim Programmaufruf übergeben. Alternativ könnte man auch eine Methode implementieren, die das Tauschverfahren bei einer Verbesserung um x Prozent beendet.
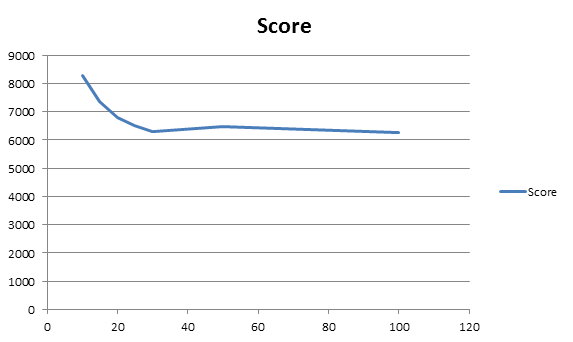
Es wurde eine Testreihe mit 6 Zügen und jeweils 50 Wiederholungen angefertigt, bei der die Tauschzahl verändert wurde.
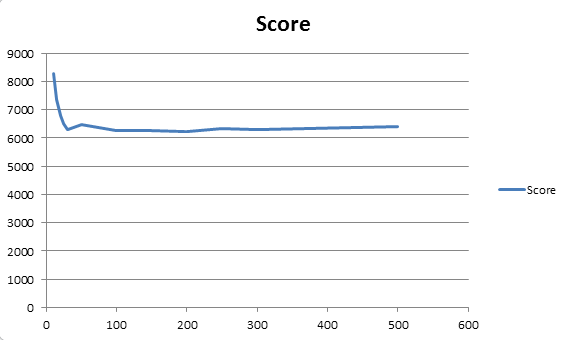 Es lässt sich schnell erkennen, dass ab etwa 75 Tauschen kaum noch Verbesserungen erzielt werden können. Die Werte darüber variieren lediglich durch die Streuung der Zufallskomponente. Deshalb sei im Anschluss noch einmal ein genauerer Blick auf das Diagramm geworfen:
Es lässt sich schnell erkennen, dass ab etwa 75 Tauschen kaum noch Verbesserungen erzielt werden können. Die Werte darüber variieren lediglich durch die Streuung der Zufallskomponente. Deshalb sei im Anschluss noch einmal ein genauerer Blick auf das Diagramm geworfen:
Diese Grafik deckt sich sehr gut mit der Beobachtung, dass selbst bei einer Tauschzahl >200 sehr selten nach mehr als 50 Versuchen noch einmal getauscht wird.
3. 3er-Tauschheuristik: Tauschen einer 3er-Kombination
Ähnlich dem obigen Algorithmus, jedoch wird eine 3er-Serie gewählt, die beste Reihenfolge der 3 Züge berechnet und dann wieder einsortiert. Hiermit lassen sich Kombinationen erzielen, die mit dem 2er-Algorithmus nie erreicht werden könnten. Aus kuriosen Gründen funktioniert dieser Algorithmus jedoch nicht, näheres im Protokoll. Quelltext
4. Simulated Annealing
Das Simulated Annealing ist eine Heuristik, die Beispielsweise für die Chipentwicklung genutzt wird. So wie bei Leiterplatten die Leiterbahnen möglichst kurz sein sollen, sollen bei uns möglichst schnell alle Züge ihren Bestimmungsort erreicht haben.
Wir erinnern uns zurück an das Modell der Landschaft: Der Algorithmus arbeitet nun ähnlich dem 2er-Tauschalgorithmus, mit einer entscheidenden Änderung: Es is dem Algorithmus möglich, auch schlechtere Zustände anzunehmen in der Hoffnung, so einem lokalen Optimum zu entkommen. In der Natur findet man Simulated Annealing bei der Abkühlung eines glühenden Metalles (daher der Name, „annealing“ ist englisch für „ausglühen“). So können Metalle beim Abkühlen einen sehr günstigen Energiezustand erreichen.
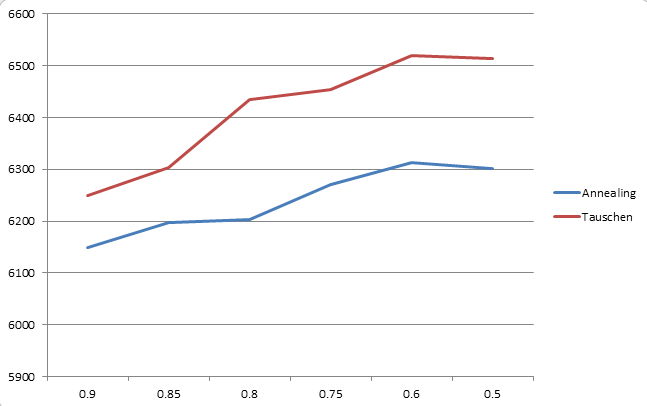
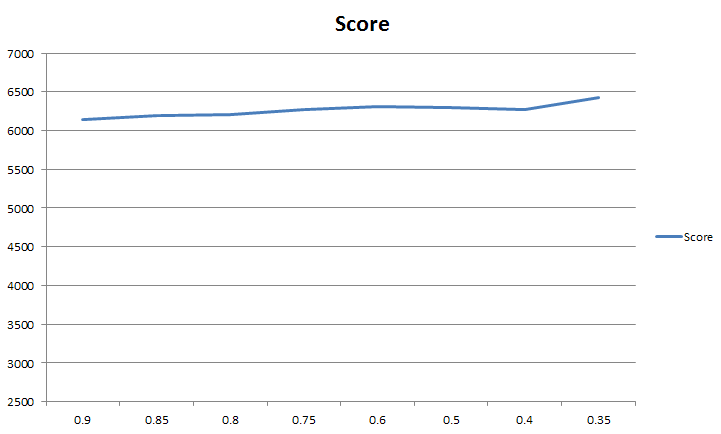
Die Sprungwahrscheinlichkeit für eine Verschlechterung ist abhängig von der „Temperatur“ des Systems, die wiederum abhängig von der Laufzeit ist (das System kühlt ab). Die Geschwindigkeit und Form dieser Abkühlung ist nun imminent wichtig für den Erfolg des Annealing-Algorithmus. Wir haben mehrere Abkühlungschemata getestet, Aufstieg bezeichnet eine Verschlechterung, Abstieg eine Verbesserung.
Grunddaten: 6 Züge Brutale Rechenzeit auf Acer c720p mit Ubuntu 14.04 in chroot-Umgebung: 8,646 s
Multiplikation mit konstantem Faktor, 50 Wiederholung, 2er-Tauschverfahren:
Es zeigt sich, dass das Annealing im Vergleich stets ein bisschen besser ist als das reine Tauschen, also alles wie erwartet. Der Unterschied ist jedoch alles andere als frappierend.
Aufgrund der Mehrfachausführung einzelner Temperaturstufen beim Annealing überträgt sich der Effekt des „Einpendelns“ der Tauschheuristik vor allem auf die schnellen Abkühlungen. Beim langsamen Abkühlen kann das Annealing jedoch seine Stärke beweisen. Besonders groß sind die Differenzen bei 6 Zügen jedoch auch noch nicht. Für das Aufstellen von Statistiken mit mehr als 6 Zügen fehlte jedoch die Rechenzeit bzw. Leistung.
Rückblick/Selbstreflektion/Ausblick
Probleme des Programms
- Das Programm ist nicht Objektorientiert geschrieben. Dies wirkte zu Beginn nicht notwendig, jedoch wuchs der Code Tumorartig in alle Richtung und selbst mit Dokumentation und Kommentaren ist es für Außenstehende wohl schwer zu verstehen.
- Wir haben viel Zeit an irritierenden Bugs verloren, trotz der „Großzügigste Schätzung * 2“-Zeitplanung
- Die Ergebnisse werden nicht sehr handlich dargestellt
Probleme vor dem Computer
- Keiner aus dem Team hat LinA belegt, was für die Algorithmenprogrammierung eine große Hürde ist
- Durch die Differenz in der Programmiererfahrung wurde viel Zeit beim erklären verloren
- Mathesis stand stets im Termin-/Prioritätenkonflikt mit Analysis und Einführung in das Verkehrswesen, welche beide vorher fällig waren.
- Nach der Mathesis-Blockveranstaltung war wieder Terminkonflikt mit Familie usw., größtes Problem war dabei viel Zeit ohne Internet, sodass nicht an der Wiki gearbeitet werden konnte.
Ausblick
- Ich selbst (Jakob) befürchte, dass wenn man wirklich weiterarbeiten wollte, ein komplettes neuschreiben des Programmes bereits mittelfristig der erste wichtige Punkt wäre, der sich dann schnell auszahlt.
Trotz allem hat das Mathesis-Labor viel Freude bereitet und war definitiv die richtige Wahl!
Protokoll
Klick: