1 Vorstellung und Grundidee
2 Verschiedene Wege zum Ziel
  2.1 Der Anfangsplan: GPS
  2.2 Erste Planänderung: Funkwellen
  2.3 Der endgültige Plan: Kameras
3 Die Umsetzung
4 Fazit

Einen Quadrocopter Fotos aus der Luft schießen lassen - das war die ursprüngliche Idee, unter der sich die Gruppe „Robotik“ in Mathesis zusammengefunden hat. Die Gruppe Robotik, das sind/waren Maximilian O., Konstantin D. und Robin N.. Natürlich gehörten zu der Idee noch viele andere Dinge: Das Gleichgewicht des Quadrocopters programmieren, feste Punkte bestimmen, die der Quadrocopter selbstständig ansteuert und - natürlich - dabei auch noch Hindernissen ausweicht. Im Endeffekt kam es doch etwas anders.

Zunächst einmal: Die Idee, das Gleichgewicht des Quadrocopters auch zu programmieren, wurde uns von Stefan und Felix relativ früh wieder ausgetrieben: Das Projekt wäre auch so schon schwierig genug, wir sollten das vorprogrammierte Gleichgewicht nehmen, war die Aussage. Es hat sich herausgestellt, dass dies ein sehr guter Rat war, denn auch so hatten wir genug zu tun.

Unsere erste Idee beinhaltete die Benutzung von GPS: Dem Quadrocopter sollten feste Koordinaten mitgegeben werden, die er mit Hilfe von GPS anfliegt. Dabei sollte eine Kamera an Bord Hindernisse erkennen und der Quadrocopter diese umfliegen. An speziellen Punkten sollten dann Bilder gemacht werden, und schließlich sollte der Quadrocopter wieder zum Start zurückkehren. Das erste Problem an diesen Plan war ein technisches: Quadrocopter sind energietechnisch sehr ungünstige Flugobjekte, die nur sehr wenig Gewicht tragen können. Von daher war es, außer mit einem sehr großen Quadrocopter, faktisch unmöglich, sowohl ein GPS-Modul als auch eine Kamera UND einen Computer auf den Quadrocopter zu tun. Für den großen Quadrocopter, der durchaus in der Uni vorhanden war, ergaben sich aber andere Schwierigkeiten: Zunächst ist dieser Quadrocopter äußerst gefährlich: Seine Rotoren sind durchaus in der Lage, Finger abzuschneiden, wenn sie dem Quadrocopter in die Quere kommen. Außerdem ist er sehr teuer - und eine Fehlfunktion, die ihn zerstört, schlicht nicht leistbar. Das nächste Problem galt für alle Quadrocopter: Für Draußen-Flüge sind Genehmigungen vonnöten. Gerade für den großen Quadrocopter werden solche Genehmigungen aber nur selten erteilt. Auch sind Quadrocopter sehr wasseranfällig und gerade im Winter daher nur schwer nutz- oder testbar. Damit war ein Draußen-Fliegen faktisch unmöglich - und daher auch die Idee mit GPS hinfällig. Eine neue Idee musste her.

Die nächste Idee war es, mit Funkwellen zu arbeiten. Das funktioniert - in einem kleinen Bereich - sowohl drinnen als auch draußen und kann somit auch im Winter mit Quadrocoptern gemacht werden. Zwei Möglichkeiten waren vorhanden: WLAN und Bluetooth. Für Bluetooth entdeckten wir bald ein Programm - - so dass wir Hoffnungen hatten, dass diese Idee funktioniert. Eine Triangulation wäre mit drei Bluetooth-Sendern möglich, ein Einblick liefert dieses kleine Programm zum Plotten:

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.path as mpath
import matplotlib.lines as mlines
import matplotlib.patches as mpatches
 
 
W = { }
N = 5
 
qx = np.random.randint(30)
qy = np.random.randint(30)
W["Referenzpunkt X"] =  qx
W["Referenzpunkt Y"] =  qy
 
plt.figure()
ax=plt.subplot(111)
ax.set_xlim([0,30])
ax.set_ylim([0,30])
ax.add_patch(mpatches.Circle((qx, qy), radius=1,color="red",alpha=0.1))
 
for i in range(0,N):                             #scatterplot handles data nonlinear, its not legible for triangulation-use
 
	x = np.random.randint(30)
	y = np.random.randint(30)
	ankathete = float(x - qx)
	gegenkathete = float(y - qy)
	radius = np.sqrt((ankathete**2) + (gegenkathete**2))
	kreisumfang = 2*np.pi*radius
	area = np.pi * (radius)**2 
	W[i] =  x,y,radius,area
 
	ax.add_patch(mpatches.Circle((x,y),radius=radius,color='blue',alpha=0.1))
	#plt.scatter(x, y, s=area*190 , alpha=0.1)
 
plt.draw()
plt.show()
print W

Bald darauf erkannten wir jedoch, dass die Entfernungsmessung viel zu ungenau funktionierte - und daher nicht in Frage kam. Also war auch diese Idee gescheitert.

An diesem Punkt erinnerten wir uns an eine Idee, die uns Stefan anfangs vermitteln wollte: Den Quadrocopter mit Hilfe von Kameras im Raum erkennen und dadurch steuern. Also vertieften wir uns in die Theorie dahinter: Wie man mit Hilfe von 2 Kameras aus 2-D Punkten 3-D Punkte zu konstruiert. Dies funktioniert zum Beispiel mit dem Lochkamera-Modell. Dieses baut darauf auf, dass Bildpunkte immer aus Linien im dreidimensionalen Raum besteht (siehe Bild). Im Schnitt zweier solcher Linien liegt also ein Punkt im dreidimensionalen. Wie man diesen Punkt bekommt - das war die Frage, die wir uns ab dann gestellt haben.

Zunächst einmal stellte sich die Frage, welche Punkte von Kameras besonders gut erkannt werden können. Nach ein wenig überlegen und den ersten (fruchtlosen) Versuchen erkannten wir, dass farbige Dioden am besten geeignet sind: Sie senden Licht in einer relativ konstanten Wellenlänge aus, die gute aus Bildern herausgefiltert werden kann. Dafür wandelt man das Bild aus dem ursprünglichen BGR-Farbraum in den HSV-Farbraum um. Der HSV-Farbraum bildet sich aus der Farbe, der Sättigung und der Helligkeit, es ist also leicht, nur Punkte mit bestimmten Werten in diesen drei Bereichen zu betrachten. Hier der Programmcode, der aus diesen Überlegungen sowie viel herumprobieren entstand. Dabei muss beachtet werden, dass für unterschiedliche Dioden und unterschiedliche Kameras unterschiedliche Ergebnisse für diese Werte erreicht werden!

import numpy as np
import cv2
import pylab
from scipy.signal import convolve2d
import threading
import time
 
#Zunächst wird mit der folgenden Definition und dem Code bis zum nächsten Kommentar ein Video hervorgerufen, bei dem jedes Kamerabild 
#den Programmcode durchläuft, angezeigt wird und danach das nächste Bild hochgeladen wird
 
def lies_kamera():
 
	global bild_aktuell
	while not stop_flag:
		print "Bild gelesen"
		res,bild_aktuell=capture.read()			
 
capture= cv2.VideoCapture(1)
stop_flag=False		
kamera_thread=threading.Thread(target=lies_kamera)
kamera_thread.start()
time.sleep(2)
 
while True:	
	bild=bild_aktuell.copy()
	cv2.namedWindow("Fenster 1")
	cv2.namedWindow("Fenster Rot")	
	cv2.namedWindow("Fenster Blau")
	cv2.imshow("Fenster 1",bild)
	cv2.waitKey(50)	
 
	#Nun wird aus dem BGR-Bild ein HSV-Bild geformt. In diesem Bild werden nun die Punkte weiß gefärbt, die zwischen den angegebenen Werten 
        #liegen, alle anderen Punkte werden schwarz gefärbt. Mit filterSpeckles werden kleine weiße Flecken bis zu einer bestimmten, selbst
        #definierten Größe, schwarz gefärbt
 
	bildhsv= cv2.cvtColor(bild,cv2.COLOR_BGR2HSV)
	bild_blau=cv2.inRange(bildhsv,np.array([100,0,200]),np.array( [110,255,255]))    #fur PS-Move
	bild_rot=cv2.inRange(bildhsv,np.array([24,0,200]),np.array( [24,255,255]))     #fur PS-Move
	cv2.filterSpeckles(bild_blau, 00, 1, 1)
 
	#Nun wird das Bild angezeigt
 
	cv2.imshow("Fenster Rot", bild_rot)													
	cv2.imshow("Fenster Blau", bild_blau)
	cv2.waitKey(30)																					
capture.release()

Nach dieser kleinen, noch unvollständigen Arbeit, beschäftigten wir uns mit der Frage, wie man aus einem gegebenen 2-D Punkt einen 3-D Punkt berechnet. Wie schon gesagt, wird dafür das Lochkamera-Modell verwendet. Dieses lässt sich auf Aufgaben aus der Linearen Algebra herunterbrechen. Im Endeffekt wird aus verschiedenen zusammengerechneten Matrizen eine finale Bildmatrix erstellt, die aus zwei 2-D Punkten in zwei Bildern einen 3-D Punkt bildet. Dafür müssen zunächst einmal die Kameras zueinander und zu sich selbst kalibriert werden. Zunächst werden Kameramatrizen K1 und K2 gesucht, die die Brennweite (Diagonale) sowie die Bildmitte (letzte Spalte) der Kamera beinhalten. Des Weiteren wird die eine Kamera in Relation zur anderen gesetzt: Der Abstand der beiden Kameras bildet einen Translationsvektor T, die Verschiebung der Koordinatensysteme, die ihren Ursprung in den jeweiligen Kameras haben, wird durch eine Rotationsmatrix R ausgeglichen. Hier der Code dazu:

#!/usr/bin/env python
# -*- coding: utf-8 -*-
#
#  unbenannt.py
#  
#  Copyright 2013 Stefan Born <born@math.tu-berlin.de>
#  
#  This program is free software; you can redistribute it and/or modify
#  it under the terms of the GNU General Public License as published by
#  the Free Software Foundation; either version 2 of the License, or
#  (at your option) any later version.
#  
#  This program is distributed in the hope that it will be useful,
#  but WITHOUT ANY WARRANTY; without even the implied warranty of
#  MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
#  GNU General Public License for more details.
#  
#  You should have received a copy of the GNU General Public License
#  along with this program; if not, write to the Free Software
#  Foundation, Inc., 51 Franklin Street, Fifth Floor, Boston,
#  MA 02110-1301, USA.
#  
#  
 
 
 
import numpy as np
import cv2
from thread import start_new_thread
from time import sleep
 
KAMERA_NR=1
STOP_FLAG=False
 
def lies_kamera():
	''' Endloschleife um Kamera auslesen;
	das zuletzt gelesene Bild befindet sich in der globalen Variable bild_aktuell'''
	global bild_aktuell
	n=0
	while not STOP_FLAG:
		n+=1
		#print "Frame " ,n
 
	# Ein Bild auslesen
		res,bild=capture.read()
		bild_aktuell=bild.copy()
 
 
 
## Kamera initialisieren
 
capture= cv2.VideoCapture(KAMERA_NR)
capture.set(cv2.cv.CV_CAP_PROP_FRAME_WIDTH,640)
capture.set(cv2.cv.CV_CAP_PROP_FRAME_HEIGHT,480)
sleep(5)
#capture.set(cv2.cv.CV_CAP_PROP_FPS,60.)
capture.set(cv2.cv.CV_CAP_PROP_SATURATION,0.1)
capture.set(cv2.cv.CV_CAP_PROP_BRIGHTNESS,0.0)
#capture.set(cv2.cv.CV_CAP_PROP_EXPOSURE,0)
start_new_thread(lies_kamera,())
sleep(2)
 
cv2.namedWindow("Bild")
 
######  Schleife, die das Schachbrettmuster im Bild sucht,
######  und die gefundenen Punkte in img_points speichert.
######  
 
abbruch=False
 
pattern_size = (9, 6)
pattern_points = np.zeros( (np.prod(pattern_size), 3), np.float32 )
pattern_points[:,:2] = np.indices(pattern_size).T.reshape(-1, 2)*2.54    
# das Kalibrierungsbrett hat 10x 7  1 inch * 1 inch-Felderpyth
 
obj_points = []
img_points = []
h, w = 0, 0
 
 
 
while not abbruch:
 
#durch ein Schachbrett bekannter Größe werden nun die vorher genannten Matrizen berechnet. Dabei werden die Abstände zwischen den Ecken der Quadrate
#gesucht und in Relation zum wahren wert gesetzt
 
	img=bild_aktuell.copy()
	gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
 
	h, w = img.shape[:2]
	found, corners = cv2.findChessboardCorners(img, pattern_size)
	if found:
		term = ( cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_COUNT, 30, 0.1 )
		cv2.cornerSubPix(gray, corners, (11, 11), (-1, -1), term)
 
		cv2.drawChessboardCorners(img, pattern_size, corners, found)
 
 
		print 'ok'
		cv2.imshow('Bild',img)
		key=cv2.waitKey(0)
		if not(key==ord('u')):
			img_points.append(corners.reshape(-1, 2))
			obj_points.append(pattern_points)	
 
		if key==ord('q'):
			abbruch=True
 
	cv2.imshow('Bild',img)	
	key=cv2.waitKey(20)
	if key==ord('q'): 
	   abbruch=True
 
camera_matrix = np.zeros((3, 3))
dist_coefs = np.zeros(4)
img_n = len(img_points)
rvecs = np.array([np.zeros(3) for i in xrange(img_n)])
tvecs = np.array([np.zeros(3) for i in xrange(img_n)])
rms, camera_matrix,dist_coefs,rvecs,tvecs = cv2.calibrateCamera(obj_points, img_points, (w, h), camera_matrix, dist_coefs , rvecs, tvecs)
print rms
print "Kamera Matrix ", camera_matrix
print "Distortion Coefficients ", dist_coefs
print "Rotation ", rvecs
print "Translation ", tvecs
cv2.destroyAllWindows()
STOP_FLAG=True

Mit diesen nun gegebenen Kameramatrizen können nun Rotationsmatrix und Translationsmatrix bestimmt werden:

import numpy as np
import cv2
import pickle
from thread import start_new_thread
from time import sleep
 
KAMERA1_NR=1
KAMERA2_NR=2
STOP_FLAG=False
 
def lies_kamera():
	''' Endloschleife um Kamera auslesen;
	das zuletzt gelesene Bild befindet sich in der globalen Variable bild_aktuell'''
	global bild1_aktuell
	global bild2_aktuell
	n=0
	while not STOP_FLAG:
		n+=1
		#print "Frame " ,n
 
	# Ein Bild auslesen
		res,bild=capture1.read()
		bild1_aktuell=bild.copy()
		res,bild=capture2.read()
		bild2_aktuell=bild.copy()
 
 
 
## Kamera initialisieren
 
capture1= cv2.VideoCapture(KAMERA1_NR)
capture1.set(cv2.cv.CV_CAP_PROP_FRAME_WIDTH,640)
capture1.set(cv2.cv.CV_CAP_PROP_FRAME_HEIGHT,480)
sleep(2)
#capture1.set(cv2.cv.CV_CAP_PROP_FPS,60.)
capture1.set(cv2.cv.CV_CAP_PROP_CONTRAST,0.1)
capture1.set(cv2.cv.CV_CAP_PROP_SATURATION,0.1)
capture1.set(cv2.cv.CV_CAP_PROP_BRIGHTNESS,0.0)
capture1.set(cv2.cv.CV_CAP_PROP_GAIN,0.1)
 
capture2= cv2.VideoCapture(KAMERA2_NR)
capture2.set(cv2.cv.CV_CAP_PROP_FRAME_WIDTH,640)
capture2.set(cv2.cv.CV_CAP_PROP_FRAME_HEIGHT,480)
sleep(2)
#capture2.set(cv2.cv.CV_CAP_PROP_FPS,60.)
capture2.set(cv2.cv.CV_CAP_PROP_CONTRAST,0.1)
capture2.set(cv2.cv.CV_CAP_PROP_SATURATION,0.1)
capture2.set(cv2.cv.CV_CAP_PROP_BRIGHTNESS,0.0)
capture2.set(cv2.cv.CV_CAP_PROP_GAIN,0.1)
#capture.set(cv2.cv.CV_CAP_PROP_EXPOSURE,0)
 
 
start_new_thread(lies_kamera,())
sleep(4)
 
cv2.namedWindow("Bild1")
cv2.namedWindow("Bild2")
 
######  Schleife, die das Schachbrettmuster im Bild sucht,
######  und die gefundenen Punkte in img_points speichert.
######  
 
abbruch=False
 
pattern_size = (9, 6)
pattern_points = np.zeros( (np.prod(pattern_size), 3), np.float32 )
pattern_points[:,:2] = np.indices(pattern_size).T.reshape(-1, 2)*2.54    
# das Kalibrierungsbrett hat 10x 7  1 inch * 1 inch-Felderpyth
 
obj_points1 = []
img_points1 = []
obj_points2 = []
img_points2 = []
 
h, w = 0, 0
 
 
 
while not abbruch:
 
	img1=bild1_aktuell.copy()
	gray1 = cv2.cvtColor(img1,cv2.COLOR_BGR2GRAY)
	img2=bild2_aktuell.copy()
	gray2 = cv2.cvtColor(img2,cv2.COLOR_BGR2GRAY)
 
 
	h, w = img1.shape[:2]
	found1, corners1 = cv2.findChessboardCorners(img1, pattern_size)
	found2, corners2 = cv2.findChessboardCorners(img2, pattern_size)
 
	if found1 and found2:
		term = ( cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_COUNT, 30, 0.1 )
		cv2.cornerSubPix(gray1, corners1, (11, 11), (-1, -1), term)
		cv2.cornerSubPix(gray2, corners2, (11, 11), (-1, -1), term)
 
		cv2.drawChessboardCorners(img1, pattern_size, corners1, found1)
		cv2.drawChessboardCorners(img2, pattern_size, corners2, found2)
 
 
 
		print 'ok'
		cv2.imshow('Bild1',img1)
		cv2.imshow('Bild2',img2)
 
		key=cv2.waitKey(0)
		if not(key==ord('u')):
			img_points1.append(corners1.reshape(-1, 2))
			obj_points1.append(pattern_points)
			img_points2.append(corners2.reshape(-1, 2))
			obj_points2.append(pattern_points)	
 
		if key==ord('q'):
			abbruch=True
 
	cv2.imshow('Bild1',img1)
	cv2.imshow('Bild2',img2)	
	key=cv2.waitKey(20)
	if key==ord('q'): 
	   abbruch=True
 
K1=file("Kameramatrix1","r")
p=pickle.Unpickler(K1)
 
camera_matrix1 = p.load()#np.array([[552.718,0.,318.714],\
#[   0. ,552.567,208.716],\
#[   0. ,0.,1.        ]])
K1.close()
K2=file("Kameramatrix2","r")
p=pickle.Unpickler(K2)
camera_matrix2= p.load()#np.array([[568.1268,0.,299.0498],\
#[   0. ,569.2292,236.8351],\
#[   0. ,0.,1.        ]])
K2.close()
 
dist_coefs1 = np.array([-0.1384 , 0.3435 , -0.0055 , 0.0060 , -0.3011])
#camera_matrix2 = np.zeros((3, 3))
dist_coefs2 = np.array([-0.1208 , 0.3704 , -0.0079 , 0.0010 , -0.3450])
#R=np.zeros((3,3))
#T=np.zeros(3)
#E=np.zeros((3,3))
#F=np.zeros((3,3))
 
img_n = len(img_points1)
#rvecs = np.array([np.zeros(3) for i in xrange(img_n)])
#tvecs = np.array([np.zeros(3) for i in xrange(img_n)])
flags = 0
flags |= cv2.CALIB_FIX_INTRINSIC
#flags |= cv2.CALIB_USE_INTRINSIC_GUESS
#flags |= cv2.CALIB_FIX_PRINCIPAL_POINT
#flags |= cv2.CALIB_FIX_FOCAL_LENGTH
flags |= cv2.CALIB_FIX_ASPECT_RATIO
flags |= cv2.CALIB_ZERO_TANGENT_DIST
flags |= cv2.CALIB_SAME_FOCAL_LENGTH
flags |= cv2.CALIB_RATIONAL_MODEL
flags |= cv2.CALIB_FIX_K3
flags |= cv2.CALIB_FIX_K4
flags |= cv2.CALIB_FIX_K5
term_crit = (cv2.TERM_CRITERIA_MAX_ITER + cv2.TERM_CRITERIA_EPS, 100, 1e-5)
 
rms, camera_matrix1,dist_coefs1,camera_matrix2, distcoefs2,R,T,E,F =\
cv2.stereoCalibrate(obj_points1, img_points1, img_points2,(w,h),cameraMatrix1=camera_matrix1,distCoeffs1=dist_coefs1, cameraMatrix2=camera_matrix2,distCoeffs2=dist_coefs2,\
criteria=term_crit,flags=flags)#,camera_matrix1,dist_coefs1,camera_matrix2,dist_coefs2,\
#R,T,E,F)
 
K1=file("Kameramatrix1","w")
p=pickle.Pickler(K1)
p.dump(camera_matrix1)
K1.close()
K2=file("Kameramatrix2","w")
p=pickle.Pickler(K2)
p.dump(camera_matrix2)
K2.close()
Rot=file("Rotationsmatrix","w")
p=pickle.Pickler(Rot)
p.dump(R)
Rot.close()
Trans=file("Translationsmatrix","w")
p=pickle.Pickler(Trans)
p.dump(T)
Trans.close()
EM=file("E","w")
p=pickle.Pickler(EM)
p.dump(E)
EM.close()
FM=file("F","w")
p=pickle.Pickler(FM)
p.dump(F)
FM.close()
Coef1=file("Coef 1","w")
p=pickle.Pickler(Coef1)
p.dump(dist_coefs1)
Coef1.close()
Coef2=file("Coef 2","w")
p=pickle.Pickler(Coef2)
p.dump(dist_coefs2)
Coef2.close()
 
print rms
print "Kamera Matrix 1", camera_matrix1
print "Kamera Matrix 2", camera_matrix2
print "Rotation ", R
print "Translation ", T
print "E ", E
print "F ", F
cv2.destroyAllWindows()
STOP_FLAG=True

Unsere Gruppe wollte sich zuerst mit dem Quadrocopter beschäftigen und dessen Gleichgewichtsstörungen beheben und danach gucken, was man noch alles implementieren könnte: z.B. eigenständig Routen abfliegen, an bestimmten Orten Aufnahmen mit einer Kamera machen oder auch ferngesteuert Fotos machen. Dafür wollten wir GPS und eine Kamera zur Kollisionserkennung benutzen.

Dann kam das Treffen mit Felix (Leiter des Robotiklabors). Der hat uns dann erstmal erklärt, dass der große Quadrocopter aufgrund seiner Größe nicht in zu kleinen Innenräumen fliegen darf, weil ihn aufgrund seiner Größe seine eigens verursachte Luftzirkulation selber behindert. Man kann ihn also in Innenräumen nicht ausprobieren. Draußen ist auch eher schlecht. Für Draußen-Flüge braucht man eine Genehmigung und generell ist das Gerät sehr wasseranfällig und sollte deshalb nach Möglichkeit nur sehr sehr wenig bis gar nicht mit ihm in Berührung kommen, was im Winter (sollte der irgendwann noch kommen) generell eher schwierig ist. Außerdem kann es bei Fehlprogrammierung durchaus vorkommen, dass der Quadrocopter ohne Möglichkeit, ihn aufzuhalten, davonfliegt und dabei sich oder anderen Schaden zufügt.

Also entfernten wir uns etwas von dem Gedanken mit diesem großen Quadrocopter uns zu beschäftigen und überlegten uns mehr mit kleineren Versionen zu arbeiten, da diese ohne große Probleme drinnen fliegen können. Damit hatten wir auch nicht mehr das Problem mit dem Gleichgewicht.

Wir hatten uns daraufhin auf das Ziel fokussiert das Fluggerät soweit zu programmieren, dass es sich eigenständig im (Innen)Raum bewegen kann und zwar ohne irgendwo gegen zu stoßen. Dafür muss es sowohl wissen, wie der Raum aussieht, als auch wo es sich selbst in diesem Raum befindet.

Seitdem haben wir uns des zweiten Teils dieses Problems angenommen: Die Ortung von sich selbst.

Unser erster Gedankenansatz lief über die Triangulation. D.h. wir haben mehrere festgesetzte Punkte, deren Standort klar ist und die messen den Abstand zu dem Fluggerät, woraus wir dessen genaue Position im Raum bestimmen können. Da wir zeitgleich das Plotten mit Python im Labor kennen gelernt haben, haben wir versucht unsere Idee zumindest im 2-dimensionalen-Raum darzustellen. Dabei hatten wir auch schon ein paar Probleme, da wir nicht genau wussten, wie die Funktion, welche wir aus dem Internet hatten funktioniert. Deshalb haben wir viel rumprobiert, bis uns Stefan eine bessere gegeben hat.

Am Ende bei rausgekommen ist folgende Funktion:

</code>

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.path as mpath
import matplotlib.lines as mlines
import matplotlib.patches as mpatches
 
 
W = { }
N = 5
 
qx = np.random.randint(30)
qy = np.random.randint(30)
W["Referenzpunkt X"] =  qx
W["Referenzpunkt Y"] =  qy
 
plt.figure()
ax=plt.subplot(111)
ax.set_xlim([0,30])
ax.set_ylim([0,30])
ax.add_patch(mpatches.Circle((qx, qy), radius=1,color="red",alpha=0.1))
 
for i in range(0,N):                             #scatterplot handles data nonlinear, its not legible for triangulation-use
 
	x = np.random.randint(30)
	y = np.random.randint(30)
	ankathete = float(x - qx)
	gegenkathete = float(y - qy)
	radius = np.sqrt((ankathete**2) + (gegenkathete**2))
	kreisumfang = 2*np.pi*radius
	area = np.pi * (radius)**2 
	W[i] =  x,y,radius,area
 
	ax.add_patch(mpatches.Circle((x,y),radius=radius,color='blue',alpha=0.1))
	#plt.scatter(x, y, s=area*190 , alpha=0.1)
 
plt.draw()
plt.show()
print W

<code>

Es wird etwas komisch angezeigt, aber wenn ihr auf bearbeiten klickt, könnt ihr, wenn ihr wollt, den Code gut rauskopieren und selbst ausprobieren.

Als wir das Grundkonzept hatten, mussten wir allerdings noch eine Möglichkeit finden das Grundkonzept technisch umzusetzen. Wir haben erst über Lichtsignale nachgedacht, haben dann ein wenig im Internet nach Möglichkeiten der Entfernungsmessung gesucht und sind dann auf WLAN und Bluetooth gestoßen. Bei Bluetooth haben wir auch gleich eine passende Mod mit Funktion gefunden und das ausprobiert

import bluetooth as bluetooth

print „performing inquiry…“

nearby_devices = bluetooth.discover_devices(lookup_names = True)

print „found %d devices“ % len(nearby_devices)

for addr, name in nearby_devices:

  print "  %s - %s" % (addr, name)

find_service(name=None, uuid=None, address=None)

Ähnliche Anzeigeprobleme: Deshalb bei Bedarf bitte wie oben. Allerdings müsst ihr vorher bluepy downloaden

Das haben wir dann mehrfach ausprobiert, aber es war deutlich zu ungenau für unsere Zwecke. Dann haben wir überlegt unsere eigene Funktion zu schreiben, durch die wir die Entfernung messen können über elektromagnetische Wellen. Diese bewegen sich aber viel zu schnell für einen Computer, um daraus vernünftige Ergebnisse raus zuziehen. Außerdem bräuchte man sehr starke Sender für die Distanz, sodass wir uns auch von dieser Idee verabschieden mussten.

Die letzte Idee war, über 2 oder mehr Kameras Dioden auf dem Quadrocopter zu erkennen und den Quadrocopter dadurch Koordinaten im von den Kameras überblickten Raum zuzuordnen. Dafür haben wir zunächst versucht, verschiedene Kameras so einzustellen, dass möglichst nur noch die Dioden auf den Bildern zu sehen waren. Dann haben wir die Bilder in den HSV-Farbraum umgewandelt, um das Bild so zu bearbeiten, dass Bildteile bestimmter Helligkeit, Farbe und Sättigung weiß und alle anderen Bildteile schwarz gefüllt werden. Dies gelang uns recht gut, einzig die Lichtbrechung an den Deckenlampen bewirkt teilweise eine Störung. Die jetzige Aufgabe ist es, die Kameras zu kalibrieren. Dafür wird mithilfe eines Schachbrettes bekannter Größe zunächst für die Kameras jeweils eine Kalibrierungsmatrix erstellt. Mit diesen Matrizen kann wird dann über die Funktion stereoCalibrate die Rotations- und Translationsmatrix und daher dann die Fundamental Matrix bestimmt.

Für alle, die, wie wir anfangs, keine Ahnung von den obigen Themen haben, hier ein kleiner Einstieg: Das Problem bei der Bestimung von Koordinaten im Raum durch Kamerabilder ist, dass die Bilder 2-dimensional, der Raum jedoch 3-dimensional ist. Alle Punkte auf dem Kamerabild entsprechen also einer Linie im Raum mit dem Ursprung in den Kamera. Gelöst werden kann das Problem durch verwenden mehrerer Kameras, die einen Punkt auch 3-dimensional erkennen können. Zunächst wird daher ein Koordinatensystem für eine Kamera aufgebaut, bestehend aus einer Kalibrierungsmatrix, die kameraspezifisch ist, und einer um eine Nullspalte erweiterte Einheitsmatrix. Dann wird ein an die erste Kamera angepasstes Koordinatensystem für die zweite Kamera aufgebaut. Dieses Koordinatensystem besteht ebenfalls aus einer Kalibrierungsmatrix, multipliziert mit einer Rotationsmatrix erweitert um eine einspaltige Translationsmatrix. Dafür muss zunächst die Drehung und der Abstand der einen Kamera zu der anderen bestimmt werden. Dafür werden die Rotations- und die Translationsmatrix benötigt. Diese werden durch Kalibrierung bestimmt, wobei die Kameras danach für den Versuch nicht mehr verschoben werden dürfen. Sie müssen also jedes mal kalibriert werden! In diesem Koordinatensystem wird jedem Punkt auf der Bildebene einer Kamera eine Linie auf der Bildebene der anderen Kamera zugeordnet. Dies kann für mehrere Punkte gemacht werden. Jede der entstehenden Linien trifft sich in einem Punkt, dem Epipolar. Dieser Punkt entspricht den Punkten auf der Bildebene der anderen ersten Kamera. Mit diesen einander zugeordneten Punkten kann man dann den 3-dimensionalen Punkt berechnen.

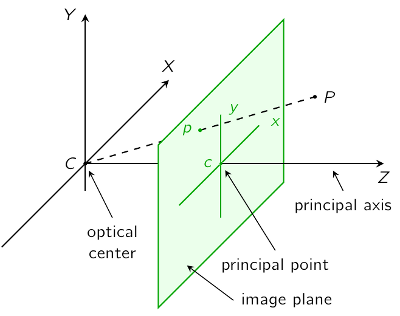Quelle: http://pille.iwr.uni-heidelberg.de/~kinect01/img/pinhole-camera.png (23.01.2014; 17:25 Uhr)

Die vorher bestimmten Matrizen werden nun mit Hilfe der Funktion stereoRectify umgeformt, um sie in der Funktion triangulatePoints endlich so zu nutzen, dass 3D-Punkte bestimmt werden können.

Soweit zur Berechnung der 3d-Punkte. Nach diesem Problem mussten wir uns wieder dem Problem der Punkterkennung widmen: Aus einem Kamerabild nötige Punkte herauszufiltern, die man in die Funktion triangulatePoints einsetzen kann.

Robotik