Quelle: de.wikipedia.org/wiki/Nichteuklidische_Geometrie

Euklid von Alexandria faste in seinem Werk „Elemente“ das mathematische Wissen von vor 2000 Jahren und seine eigenen Erkenntnisse zusammen.¹⁾ Besonders bekannt ist seine Geometrie. Nach ein paar Definitionen und Axiomen folgen 5 Postulate:

Euklid postuliert,²⁾

• dass man von jedem Punkt nach jedem Punkt die Strecke ziehen könne,
• dass man eine begrenzte gerade Linie zusammenhängend gerade verlängern könne,
• dass man mit jedem Mittelpunkt und Abstand den Kreis zeichnen könne,
• dass alle rechten Winkel einander gleich seien,
• dass, wenn eine gerade Linie beim Schnitt mit zwei geraden Linien bewirke, dass innen auf derselben Seite entstehende Winkel zusammen kleiner als zwei Rechte würden, dann die zwei geraden Linien bei Verlängerung ins Unendliche sich treffen würden auf der Seite, auf der die Winkel lägen, die zusammen kleiner als zwei rechte seien

Wie man sehen kann, ist das 5. Postulat nicht so kurz und elegant wie die anderen. Es ist in textform auch sehr kompliziert.

Quelle: de.wikipedia.org/wiki/Euklid

Kurzgefasst sagt das 5. Postulat:
Da auf der linken Seite von s die beiden Winkel zusammen kleiner als 180° sind, so müssen sich die geraden g und h auch auf dieser Seite schneiden. Oder noch allgemeiner: Es existieren Parallelen.

Wahrscheinlich hätte Euklid das auch lieber als einen Satz bewiesen, nur leider folgt das 5. Postulat nicht aus den anderen. Gegenbeispiele finden sich in der nichteuklidischen Geometrie.

Befindet man sich zum Beispiel auf einer Kugeloberfläche, so erkennt man leicht, dass sich die geraden unabhängig von der Winkelsumme immer auf beiden Seiten schneiden und somit das 5. Postulat verletzen.

Quelle: de.wikipedia.org/wiki/Nichteuklidische_Geometrie

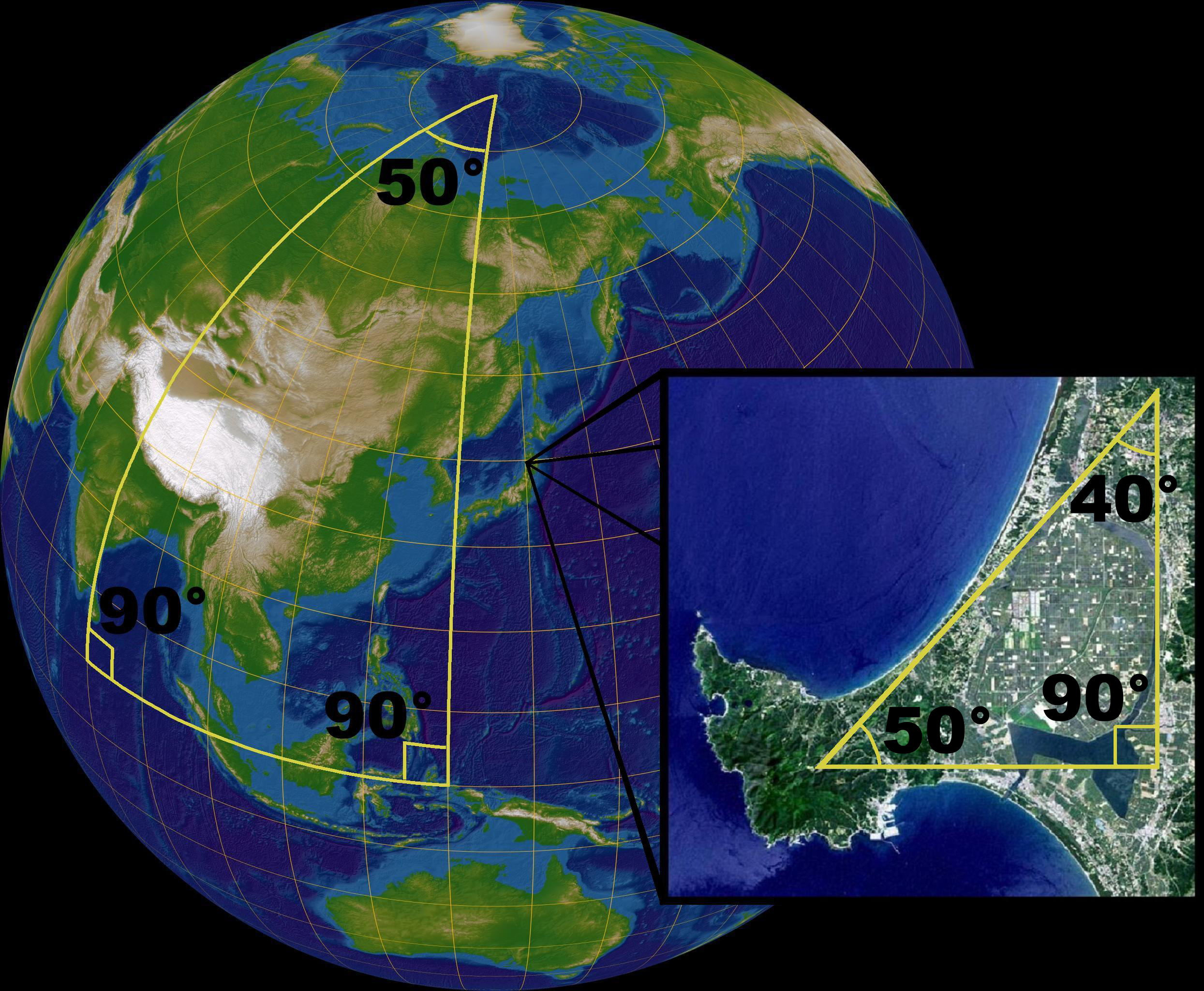
Eine Eigenschaft des elliptischen Raumes ist, dass die Innenwinkelsumme eines Dreieckes immer mehr als 180° beträgt. Davon bemerken wir im Alltag nichts, vermisst man aber ein großes dreieckiges Stück Land, so machen sich die elliptischen Eigenschaften der Erdoberfläche bemerkbar.

Befindet man sich in einem hyperbolischen Raum, so kann es sein, dass sich zwei Geraden trotz einer Winkelsumme weniger als 180° gar nicht schneiden und somit offensichtlich dem 5. Postulat widersprechen.

Quelle: youtu.be/zQo_S3yNa2w

Einen zweidimensionalen euklidischen Raum kann man in ein quadratisches Raster unterteilen, sodass immer 4 Quadrate sich einen Eckpunkt teilen. Dies ist der Fall, da 4 mal 90° einen Vollwinkel ergibt. In diesem Beispiel eines hyperbolischen Raumes passen allerdings 5 Quadrate um einen Eckpunkt. Somit könnte man dieses Gebilde nicht mehr „flach auf einen Tisch legen“, es muss also in einer höheren Dimension gekrümmt sein.

Wie in der elyptischen und hyperbolischen Geometrie zu sehen, sind die Oberflächen beliebiger höherdimensionaler gekrümmter Objekte nichteuklidische Räume. Man muss allerdings garnichts kompliziertes konstruieren, um einen Raum zu erhalten, der das 5. Postulat missachtet. Ein Raum könnte beispielsweise in seiner Größe begrenzt sein. So kann das Ende erreicht werden, bevor sich die Linien schneiden würden. Ein weiterer vergleichsweise einfach zu verstehender Raum ist einer, der Portale zulässt.

Quelle: https://youtu.be/kEB11PQ9Eo8

Stellt man sich ein Portal als ein Schnitt im Raum vor, der mit einem anderen Ort wieder zusammengeklebt wurde, so kann man viele Eigenschaften höherdimensionaler Oberflächen nachstellen. Nimmt man einen rechteckigen Raum und verbindet das linke und rechte Ende mit Portalen, so erhällt man einen Ring. Verbindet man nun auch noch oben mit unten erhält man einen Torsus.

↑ Zurück nach oben