Benutzer-Werkzeuge
Seitenleiste
Dies ist eine alte Version des Dokuments!
Inhaltsverzeichnis
Research
Euklidische Geometrie
Euklid von Alexandria fasste in seinem Werk „Elemente“ das mathematische Wissen von vor 2000 Jahren und seine eigenen Erkenntnisse zusammen.1) Besonders bekannt ist seine Geometrie. Nach ein paar Definitionen und Axiomen folgen 5 Postullate:
Euklid postuliert,2)
- dass man von jedem Punkt nach jedem Punkt die Strecke ziehen könne,
- dass man eine begrenzte gerade Linie zusammenhängend gerade verlängern könne,
- dass man mit jedem Mittelpunkt und Abstand den Kreis zeichnen könne,
- dass alle rechten Winkel einander gleich seien,
- dass, wenn eine gerade Linie beim Schnitt mit zwei geraden Linien bewirke, dass innen auf derselben Seite entstehende Winkel zusammen kleiner als zwei Rechte würden, dann die zwei geraden Linien bei Verlängerung ins Unendliche sich treffen würden auf der Seite, auf der die Winkel lägen, die zusammen kleiner als zwei rechte seien
Wie man sehen kann, ist das 5. Postulat nicht so kurz und elegant, wie die anderen. Es ist in textform auch sehr kompliziert.

Quelle: de.wikipedia.org/wiki/Euklid
Kurzgefasst sagt das 5. Postulat: Da auf der linken Seite von s die beiden Winkel zusammen kleiner als 180° sind, so müssen sich die geraden g und h auch auf dieser Seite schneiden. Oder noch allgemeiner: Es existieren Paralelen.
Warscheinlich hätte Euklid das auch lieber als einen Satz bewiesen, nur leider folgt das 5. Postullat nicht aus den ersten 4. Gegenbeispiele finden sich in der Nichteuklidischen Geometrie.
Nichteuklidische Geometrie
Elyptisch
Befindet man sich zum Beispiel auf einer Kugeloberfläche, so erkännt man leicht, dass sich die geraden unabhängig von der Winkelsumme immer auf beiden Seiten schneiden und somit das 5. Postulat verletzen.
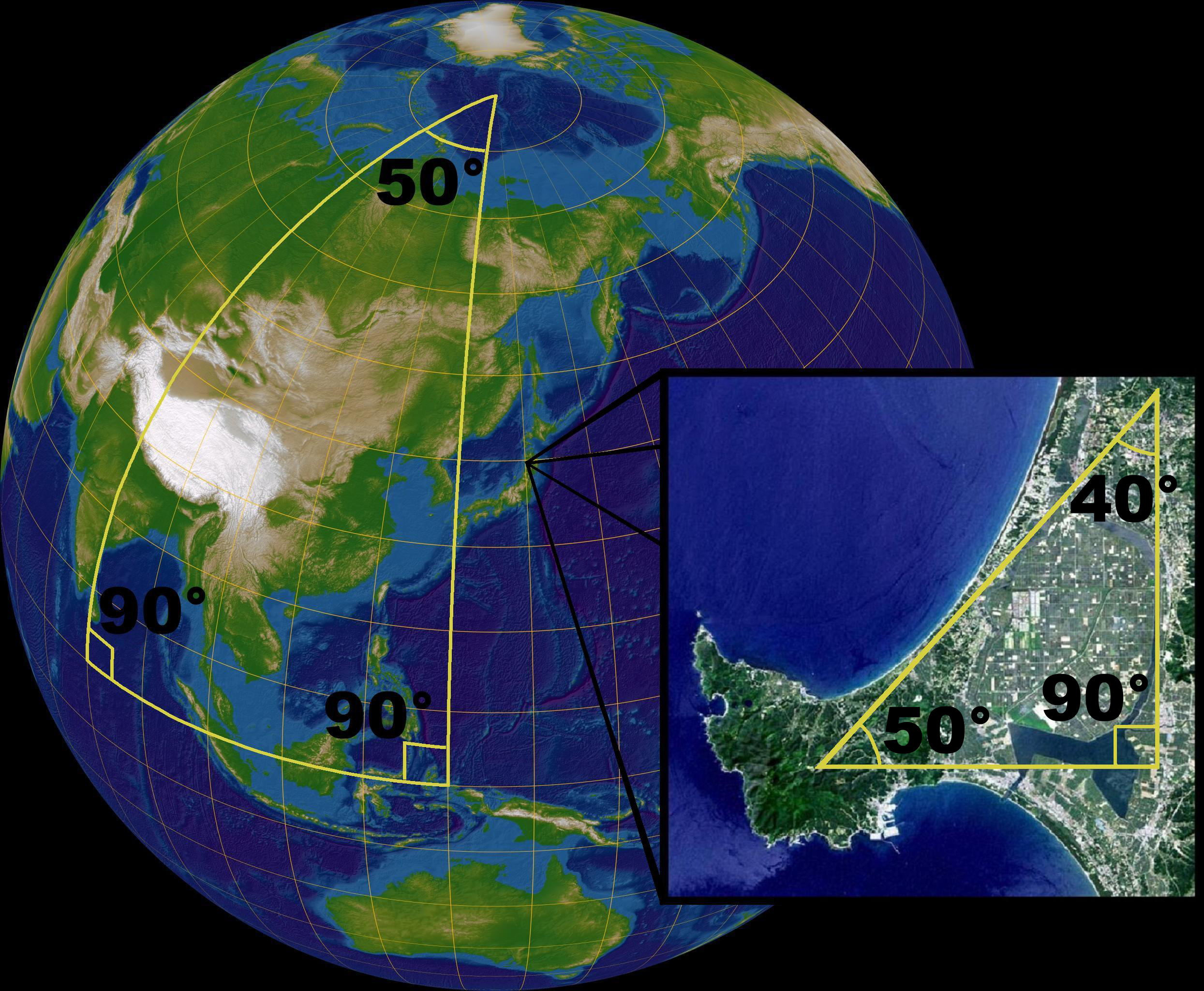
Quelle: de.wikipedia.org/wiki/Nichteuklidische_Geometrie
Eine Eigenschaft des elyptischen Raumes ist, dass die Innenwinkelsumme eines Dreieckes immer mehr als 180° bebträgt. Davon bemerken wir im Alltag nichts, vermisst man aber ein großes dreieckiges Stück Land, so machen sich die elyptischen Eigenschaften der Erdöberfläche bemerkbar.
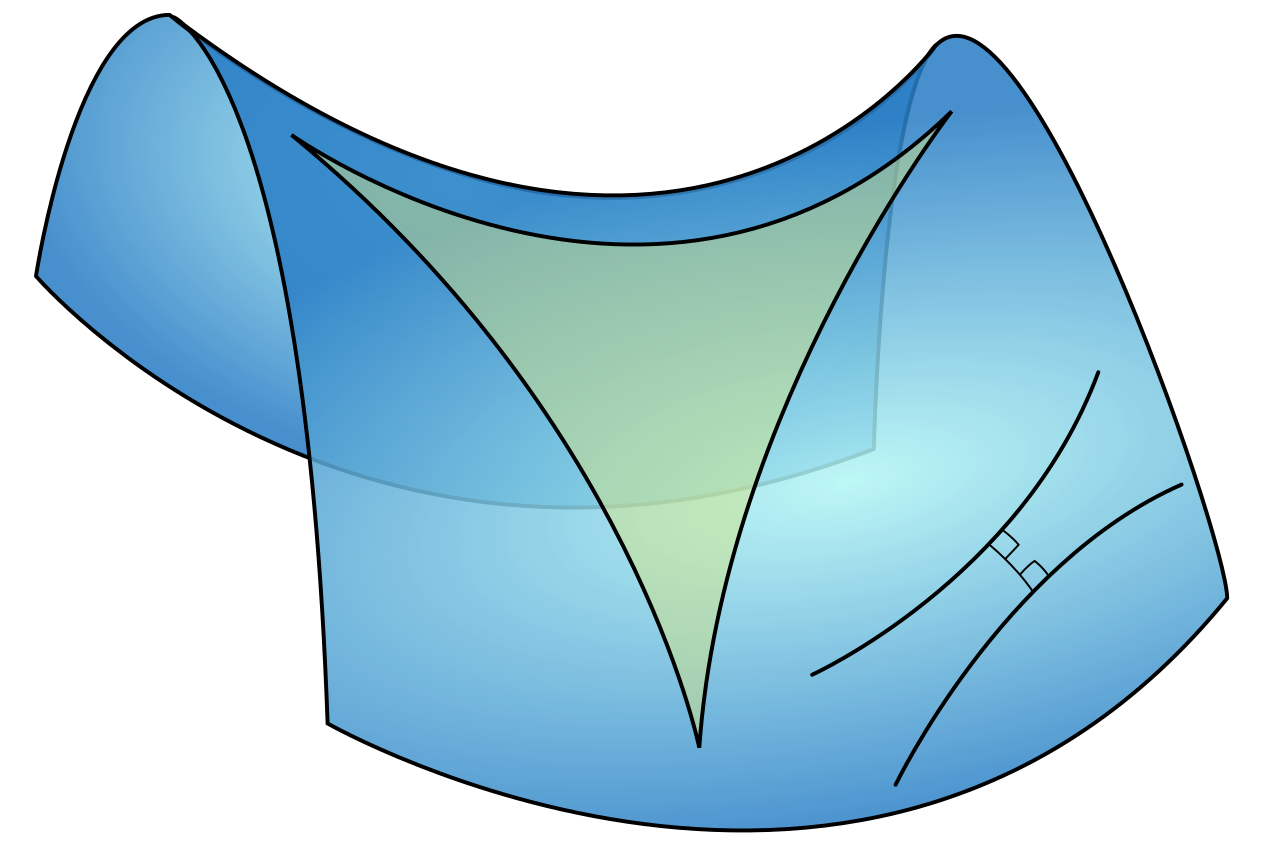
Hyperbolisch
z. B. Sattelfläche
Weitere Formen
z. B. oberflächen beliebiger höherdimensionaler objekte, diese lassen auch dinge wie portale oder repetetive welten zu
Quelle: youtube.com/CodeParade