Die Darstellung gefällt mir gut, in diesem Fall finde ich es überzeugend, die Erzählung vom Projektverlauf nicht von der Darstellung zu trennen. Die Darstellung der Dateiformat- Entwicklung, der Wegfinde-Algorithmen und der Optimierung sind durchweg erfreulich

Zweierlei würde ich mir noch wünschen:

• Der Code selbst sollte von der Dokumentation aus zugänglich sein. Das kann entweder in einzelnen Seiten in <code python> </code> -tags erfolgen oder durch Verlinken auf ein (einigermaßen augeräumtes) gitlab/github/tubcloud Verzeichnis. Das letztere hat den Vorteil, dass dort auch eure geputzten Daten Platz finden würden, die ja auch für andere interessant wären.
  Ach ja, es gäbe noch die dritte Variante, eure Programm-Dateien zu zippen und das zip in der Wiki hochzuladen. In allen Fällen wäre es gut, wenn es ein kleines Inhaltsverzeichnis des Codes gibt, d.h. welche Programme es überhaupt gibt. mit eurer Erlaubnis auch ein gitlab-Verzeichnis anlegen.

• Ein kleines Fazit.

• Felix Henze
• Marvin Randig

Volksentscheid Fahrrad: Die Medien berichten täglich über ihn. die ganze Stadt spricht darüber und er sorgt regelmäßig für lebhafte Debatten im Senat. Fakt ist: Das Radwegenetz ist in einem miserablen Zustand, wie wir es jeden Tag erneut spüren dürfen. Ein Ausbau ist dringend erforderlich. Für eine moderne, mobile Stadt ohne Verkehrsprobleme und mit gesunden Bürgern. Dies wäre eine zukunftsorientierte Investition in die Infrastruktur, die u. a. schon in Kopenhagen auf Wunsch der Bürger höchst erfolgreich vollzogen wurde und dort nun den Haushalt und die Menschen entlastet. Doch wie soll der Ausbau vonstatten gehen? Berliner Infrastrukturprojekte sind schließlich derzeit gemeinhin nicht für angemessene Planung bekannt. Deshalb haben wir uns zum Ziel gesetzt, das Problem zu simulieren und eine möglichst optimale Lösung zu finden.

Ziel des Projekts ist es, eine möglichst optimale Verkehrswegeplanung zu erstellen. Dies kann für Radwege geschehen, aber auch auf Straßen, Wasserrohre Datenleitungen o. Ä. verallgemeinert werden. Hierfür müssen vielerlei Kriterien beachtet werden. Außerdem sind mehrere Varianten der Optimierung denkbar: auf Kosten, Verfügbarkeit, Kapazität, „Geschwindigkeit“, ebenso sind auch Mischkriterien denkbar.

Wichtige Themenfelder für das Projekt sind: verschiedene Formen der Optimierung, Graphentheorie, objektorientierte Programmierung sowie die Einbindung von Kartendaten.

Der Grunddatensatz für das Berliner Verkehrsnetz ließ sich recht einfach von openstreetmap.org herunterladen. Leider belief sich der ausgewählte Bereich auf eine Dateiengröße von ~1.6 GB, was eine Weile braucht, um es in Python zu laden. Deshalb wurde der Datensatz in zwei Schritten verkleinert. Erst wurden durch das Kommandozeilen-tool Osmosis (ebenfalls von openstreetmap) alle Straßen und Standpunkte, die nicht mit dem Fahrrad befahrbar sind, (Autobahn, Flughafen, etc.) gelöscht. Beim zweiten Schritt wurden nicht brauchbare Meta-Informationen und unnötige Tags mit eigenen python-Skripten entfernt. Im Laufe dessen ergab es sich, ein eigenes Dateiformat zu erstellen um die Daten einfacher und schneller lesen/schreiben zu können. Diese Datei hatte am Ende dann nur noch eine Größe von ~67 MB.
Dateiformat-Entwicklung

Um mit den Daten einfach arbeiten zu können, wurden diese als Graph gespeichert. Dafür wurden 3 Objektklassen erstellt: die Node-Klasse (Knoten), die Edge-Klasse (Kante), und die Graph-Klasse. Ein Graph besteht aus Knoten und Kanten, wobei Kanten die Verbindungen zwischen Knoten darstellen. Im Fall des Verkehrsnetzes wäre das dann z.B. eine Straße als Verbindung zwischen zwei Kreuzungen. Mit diesen drei Klassen konnten dann die Daten eingelesen und damit gearbeitet werden.

Der Dijkstra-Algorithmus ist möglicherweise der grundlegendste Algorithmus in der Graphentheorie. Er berechnet von einem Knoten aus über die Kanten die jeweils kürzeste Weglänge zu allen anderen (erreichbaren) Knoten aus. Dies macht er, indem die Nachbarn vom aktuellen Knoten anhand der Kantenentfernung in eine Liste einordnet (kürzeste=Vorne, längste=Hinten). Nachdem er alle Nachbarn in die Liste eingefügt hat, wird der erste Knoten der Liste als aktuelles Element herausgenommen und das ganze geschieht von vorne. Wenn ein Zielknoten gegeben ist, läuft der Algorithmus bis er den Zielknoten als Nachbarn findet, wenn nicht läuft er bis allen (erreichbaren) Knoten ihre Entfernung zugewiesen wurde. (Code-Schnipsel vom Dijkstra-Algorithmus einfügen?)
Wie man sich vorstellen kann, muss der Algorithmus gegebenfalls sehr viele Knoten durchlaufen bis er das Ziel erreicht, was zu einer recht hohen Laufzeit führen kann. Deswegen wurde der A*-Algorithmus in betracht bezogen, der eine Erweiterung des Dijkstra-Algorithmus ist. Beim A* wird beim einordnen in die Liste noch die abgeschätzte Distanz von aktuellem Knoten zu Ziel mit einberechnet. In diesem Fall ist die abgeschätzte Distanz die Länge der Fluglinie zwischen Knoten und Ziel. Das heißt im Grunde, dass sich der A*-Algorithmus schneller in die Richtung des Ziels geht und somit eine schnellere Laufzeit hat.

Hier ist der gleiche Pfad in einem Gittergraph einmal mit Dijkstra (links) und einmal mit A*(rechts). Die grauen Pixel sind die besuchten Knoten und die roten Pixel ergeben den gefundenen Pfad.

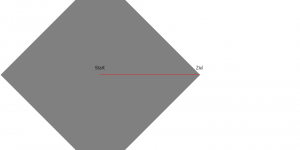
Wie man sehen kann, besucht A* sehr viel weniger Knoten als Dijkstra und hat somit eine sehr viel kleinere Laufzeit. Bei Graphen in denen die Knoten nicht so ein homogenes Gitter sind (wie zum Beispiel ein Verkehrsnetz) kann diese geringe Anzahl der besuchten Knoten dazu führen, das nicht der kürzeste Weg gefunden wird. Deswegen wurde eine weight-Variable eingefügt, die bestimmt wie groß der Einfluss der abgeschätzen Distanz auf die Einordung in die Liste ist (0.0-1.0).
A* mit weight=0.5:

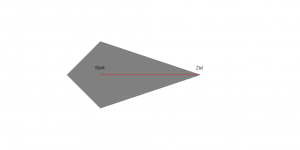
Bei den Tests wurden zufällige Knotenpaare ausgewählt und dann die gefundene Distanz von Dijkstra mit der gefundenen Distanz von A* (mit verschiedenen Gewichtungen) vergleicht. Bei den folgenden Graphen ist die x-Achse der Wert der weight-Variable. Der rote Strich ist die gefundene Weglänge relativ zu Dijkstra (1.0 → Dijkstra=A*) und der blaue Strich ist die Anzahl der besuchten Nodes (auch relativ zu Dijkstra) was proportional der Laufzeit entspricht.

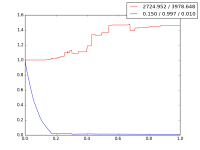
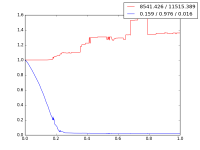
Mit einigen weiteren Test (die sich auf das kritische Gebiet konzentrierten aber keine hübschen Graphen lieferten) ließ sich schließen, dass alle Weglängenunterschiede unter einem Gewicht von 0.1 vernachlässigbar sind (<1m) und dieser Wert gut für diese Situation gewählt ist.

Zur Bewertung eines Graphen wurde folgendes System herangezogen:

• Zunächst wurden die für den Fahrradverkahr wichtigsten Knotenpunkte aus dem Kartengebiet bestimmt.
• Dazu wurde eine größere, zweite Menge an Knoten zufällig ausgewählt. Diese Knoten modellieren die Bevölkerung (Radfahrer). Hierbei wurde festgestellt, dass eine Gewichtung mit der Bevölkerungsdichte nicht zwingend notwendig ist, da die Anzahl der Knoten in dicht besidelten Gebieten zumeist auch höher ist.
• Dann wurden die Längen der Wege zwischen jedem der zuerst ausgewählten und jedem der später ausgewählten Knoten, sofern diese über das Netz verbunden waren, berechnet.
• Die Mittelung dieser Werte ergab dann eine Bewertung des Netzwerkes.
• Anmerkung: Da der Dijkstra-Algorithmus nicht nur die Entfernung zweier Knoten, sondern auch ohne viel Mehraufwand von einem gemeinsamen Knoten ausgehend die Entfernung aller Knoten von diesem Knoten berechnen kann, ist die Laufzeit des Bewertungsverfahren hauptsächlich abhängig von der Anzahl der zuerst ausgewählten Knoten. Die Anzahl der später ausgewählten Knoten spielt eine eher untergeordnete Rolle.

Mithilfe dieses Bewertungssystems konnte nun eine mehrstufige Optimierung des Graphen vorgenommen werden. Diese sollte in Abhängigkeit eines vorgebenen maximalen Kostenbetrags einen möglichst guten Ausbau des Radwegenetzes bestimmen. Hierbei wurde wie folgt vorgegangen:

• Zunächst wurden nur die Wege zwischen den sehr wichtigen, zuerst ausgewählten, Knotenpunkten betrachtet. Bei diesen wurde bestimmt, welche Wegstecken am häufigsten auf kürzesten Wegen enthalten sind. Diese wurden für einen Ausbau in Betracht gezogen. Um zu bestimmen, welche dieser Wegstrecken tatsächlich ausgebaut werden sollten, wurden die Häufigkeiten der Verwendung in Relation zu den Kosten gesetzt um so eine wirtschaftliche Optimierung vorzunehmen.
• Nach diesem Ausbau wurde erneut überprüft, welche Wege am häufigsten Verwendung finden, da sich dies durch den Aubau verändert haben könnte. Es folgte eine erneute Überprüfung auf Wirtschaflichkeit und der Ausbau der am besten geeigneten Wege.
• Diese Prozedur wurde so noch einige Male wiederholt, bis die Wege zwischen den wichtigsten Knkotenpunkten einen guten Ausbauzustand erreichten.
• Darauf folgte eine Zerlegung des Gesamtgraphen in mehrere Teilgraphen, in denen durch eine wesentlich verringerte Anzahl an Knoten und Kanten eine bessere Optimierung möglich ist.
• In diesen Teilgraphen wurden wieder mehrfach die wichtigsten und wirschaftlichsten Wege bstimmt und ausgebaut.

Dieser Ausbau kann vollzogen werden solange noch genügend Geld hierfür vorhanden ist. Danach kann die Güte des Netzes erneut bewertet werden und so können benötigten Kosten eine zu erwartetende Zeitersparnis zugeordnet werden. Nach dem Ausbau kann das ausgebaute Netz mittels Maperitive veranschaulicht werden

Da die Kosten für einen Ausbau eines Fahrradweges je nach Quelle variieren, nahmen wir zunächst fiktive Daten für die Bestimmung der Einheitskosten für die verschiedenen Stufen des Ausbaus. Die Kosten für den Ausbau einer Teilstrecke ergaben sich dann als Produkt von Länge und Einheitskosten sowie eventuell einem „Anfangssummanden“, falls die Teilstrecke am Anfang oder Ende einer ausgebauten Strecke liegt. Dies verhindert das Zersplittern der ausgebauten Teile und sorgt für eher zusammenhängende ausgebaute Strecken, welche die Kosten reduzieren.

* Protokoll 1 (26.05.2016)
* Protokoll 2 (02.06.2016)
* Protokoll 3 (09.06.2016)
* Protokoll 4 (16.06.2016)
* Protokoll 5 (23.06.2016)
* Protokoll 6 (30.06.2016)
* Protokoll 7 (07.07.2016)
* Protokoll 8 (14.07.2016)
* Protokoll 9 (21.07.2016)
* Protokoll 10 (31.08.2016)
* Protokoll 11 (01.09.2016)
* Protokoll 12 (02.09.2016)